Verifique se é razoável considerar um modelo de regressão linear relacionando as notas de inglês e Português , segundo os dados apresentados na tabela a seguir. Sua conclusão deve ser baseada no coeficiente de correlação e no ajuste da reta de regressão.

Para realizar o teste precisamos montar uma tabela de regressão linear, do tipo:

Basicamente, obtendo esses três valores de , podemos montar a tabela e concluir o teste.

Vale lembrar, que é o número de variáveis então no nosso caso, ; e além disso, representa o tamanho da nossa amostra, temos .

Repare ainda que vamos precisar, utilizando a estimação que fizemos para a reta, obter todos os ; em outras palavras:

E assim por diante, até:

Coloquei todos os valores na tabelinha abaixo, confere se bateu com o seu:

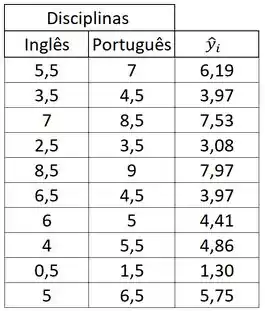
Tá comigo?? Let’s bora!

Agora podemos encontrar as somas de quadrados:

E por último:

Agora, olhando o modelo de tabela que mostrei antes, fica fácil achar os quadrados médios (QM); teremos a seguinte tabela de regressão linear:

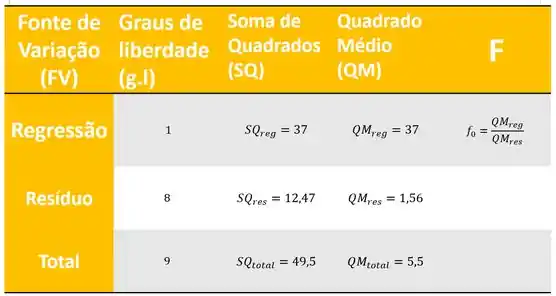
Ainda falta realizar o teste, lembrando que devemos utilizar a seguinte aproximação:

Chamamos essa distribuição de com graus de liberdade.

Antes de finalmente realizarmos o teste, vamos deixar bem definida quem é nossa região crítica quando adotamos :

Portanto, deveremos buscar na tabela um valor tal que:

Para achar a resposta certa devemos procurar na tabela de 5%, na coluna de grau de liberdade e na linha de graus de liberdade:

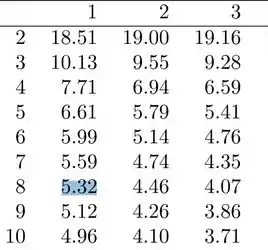
Achou aí?? Nossa região crítica fica assim:

Agora, graças a sua paciência, podemos realizar o teste:

Percebeu que pertence a nossa região crítica?! Então sempre que isso acontecer vamos rejeitar a hipótese nula.

Mas peraí, quem era a nossa hipótese mesmo?? Foram tantas informações né... mas vamos lá:

Definimos , ao rejeitarmos essa hipótese, estamos afirmando que é verdade.

Logo, como o representa o coeficiente angular da reta, o fato de ele ser realmente diferente de zero nos diz que as duas disciplinas têm entre si uma relação de linearidade.