Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.2 - Ex. 2
Sabe-se que o tempo necessário para percorrer uma determinada rota no final da tarde pode ser estudado por um modelo Normal com desvio padrão de 17 minutos. Foram instalados sensores para controlar o tempo de abertura dos semáforos presentes na rota e deseja-se verificar se o tempo gasto para completar o percurso diminuiu. Estudos anteriores indicam que o tempo de deve continuar se comportando segundo um modelo Normal, com mesmo desvio padrão. Com os sensores desativados, 11 veículos de mesmo ano e marca, denominado Grupo de Controle, tiveram o tempo gasto no percurso anotado. Em seguida, os sensores foram ativados e outros 13 veículos (grupo teste) percorreram a mesma rota. Os tempos observados, em minutos, foram os seguintes:
Indique se o uso dos sensores contribui para diminuir o tempo médio de percurso utilizando o nível descritivo do teste.
Passo 1
Caraca, mó textão de facebook, então tá neh!
Mas perceba que a única coisa que ele quis dizer é que precisamos testar se o tempo médio gasto no percurso é diminuído após a aplicação dos sensores.
Antes de seguir, vamos definir nossa variável:
Beleza, só que quando fazemos comparações de médias antes de mais nada temos sempre que perguntar sobre a variância; repara que o enunciado deixa a entender que, COM OU SEM o sensor, o desvio padrão é 17 minutos.
Isso significa então que trata-se de um teste para a média de duas populações com variâncias conhecidas e iguais; então utilizaremos a seguinte aproximação pela normal padrão:
Onde conhecemos as variâncias populacionais e os tamanhos de cada amostra:
E
Falta obtermos a média amostral:
E
Passo 2
Vamos definir de umavez por todas quem são as nossas hipóteses:
Por que? Ora pois, porque queremos saber se o tempo gasto no grupo de teste realmente foi menor do que no grupo de controle. Se eu rejeito então posso afirmar que a média realmente foi menor após os sensores; caso contrário, eu aceito e afirmo que elas se manteram pelo menos iguais.
Feito isso, como o enunciado pede para usarmos nível descritivo, vamos relembrar do que se trata.
Bom o nível descritivo nada mais é do que a chance de a gente achar um valor mais extremo do que o obtido no teste; em outras palavras:
Passo 3
Huuuum! Mas quem é aquele zezinho alí? Ele é a estatística do teste, encontramos ele realizando o teste sob . Vamos a isso então:
Como em , :
Ou seja, queremos encontrar:
Para isso, basta irmos na tabela de distribuição Normal:
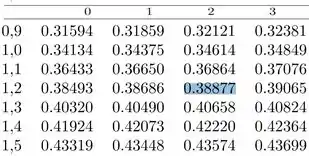
Portanto:
Mas cuidado!! Essa ainda não é a resposta, pois todo o corpo da tabela fornece as probabilidades de:
Como queremos a chance de ser maior do que e lembrando que o gráfico da normal possui cada metade valendo 0,5 então devemos fazer o seguinte:
E então:
Agora, você lembra que para valores muito pequenos de nível descritivo nós rejeitamos ? Mas a gente encontrou , o que não podemos considerar como sendo um valor pequeno.
Se você ainda não está convencido de que 11% não é um valor pequeno, basta você lembrar que quase sempre a gente considera um nível de significância de 5%; e que quando:
Nós devemos ACEITAR a hipótese nula; , certo? Então vamos aceitar .
Resposta
Podemos concluir que muito provavelmente os sensores não foram eficientes em reduzir o tempo necessário para a realização do percurso.