Em um estudo para estimar a proporção de esposas que assistem a novelas regularmente, descobre-se que 52 de 200 esposas em Denver, 31 de 150 em Phoenix e 37 de 150 em Rochester assistem a pelo menos uma novela. Use um nível de significância de 0,05 para testar a hipótese de que não há diferença entre as reais proporções de esposas que assistem a novelas nas três cidades.
Passo 1
Falaaaa moçadinha, show de bola?
Como diz o Homem de ferro “Eu tenho um plano. Ataque!”

Bora atacar esse problemaaaaaaa junto comigoo.
Sejam as proporções de esposas que assistem novelas nas três cidades respectivamente
O nível de significância especificado é
Vamos considerar a seguinte tabela
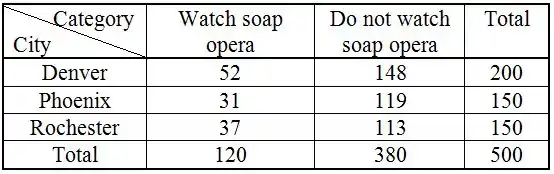
A regra geral para obtenção da frequência esperada de qualquer célula é dada pela seguinte maneira:
Na tabela a seguir, mostraremos a frequência observada junto com a frequência esperada ente colchetes para cada célula
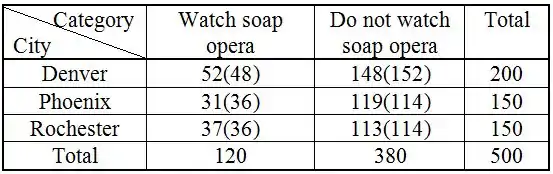
A estatística do teste qui-quadrado é dada como
Sob a estatística de teste segue a distribuição de com graus de liberdade, pois há duas linhas e duas colunas.
Passo 2
A região crítica é dada como onde é o ponto 0.05 superior da distribuição com 2 graus de liberdade.
Portanto, não rejeite e concluímos que não há diferença entre as verdadeiras proporções de esposas que assistem novelas nessas três cidades.
“Às vezes é preciso aprender a correr antes de começar a andar”

Resposta
Portanto, não rejeite e concluímos que não há diferença entre as verdadeiras proporções de esposas que assistem novelas nessas três cidades.