Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 78

Sabemos que as emissões de hidrocarboneto decresceram drasticamente durante os anos 1980. Um estudo foi conduzido para comparar as emissões de hidrocarboneto, em partes por milhão (ppm), para automóveis dos anos 1980 e 1990 quando em marcha lenta. Vinte carros de cada ano foram selecionados aleatoriamente e os níveis foram comparados. Os dados são os seguintes:

Teste a hipótese de que σ 1 = σ 2 contra a alternativa de que σ 1 ≠ σ 2 . Assuma que ambas as populações são normais. Use um valor P.

Passo 1

E ai seres de luz, tudo bem?

Como diz o Homer “Filho, este aparelhinho vai nos ajudar a escapar dessa fria!”

Os dados a seguir fornecem os níveis de emissão de hidrocarbonetos para vinte carros de cada ano modelo.

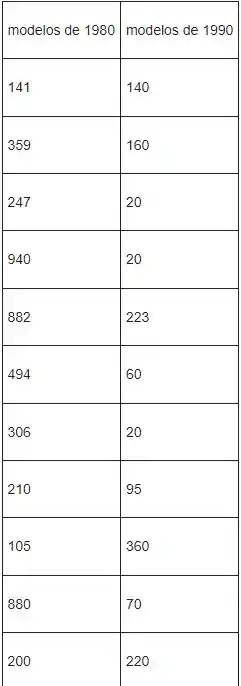
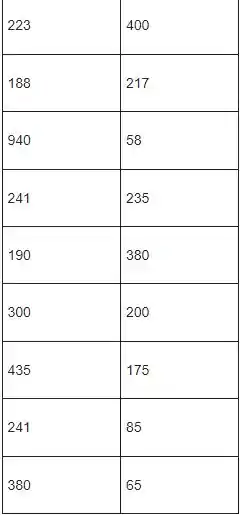
Reivindicação: Podemos aplicar o teste F para testar desvios padrão. Agora organizamos o procedimento de teste e os cálculos são fornecidos abaixo.

Procedimento:

A hipótese nula e alternativa é

H 0 : σ 1 = σ 2

H 1 : σ 1 ≠ σ 2

Nivel de significância, α   =   0.05 .

A estatística de teste computada é então dada por,

f = s 1 2 s 2 2

Onde s 1 2   e   s 2 2   estão as variações calculadas a partir das duas amostras. Se as duas populações forem aproximadamente normalmente distribuídas e a hipótese nula for verdadeira, a razão ƒ   =   s 1 2 / s 2 2   é um valor da distribuição F com v 1 = n 1 - 1   a n d   v 2 =   n 2 -   1 graus de liberdade. Para a alternativa bilateral, a região crítica é f < f 1 - α / 2 ( v 1 , v 2 ) ou f < f α / 2 ( v 1 , v 2 )

Passo 2

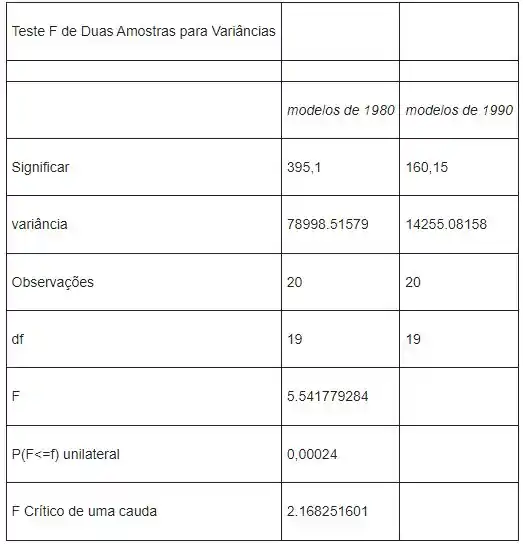
Decisão: A partir da saída, a estatística de teste e o valor P ƒ   =   5.54   b i c a u d a l   =   2 ( 0,0002 )   =

0,0004 é menor que o nível de significância, rejeitamos a hipótese nula e concluímos que no nível de 5%, e afirmamos que as variâncias pois os dois modelos são significativamente diferentes.

“Eu não estava mentindo! Estava escrevendo ficção com a boca.”

Resposta

Resposta nos passos

Exercícios de Livros Relacionados

Sabemos que o volume dos recipientes de certo lubrificante é normalmente distribuído com variância de 0,03 litro. Teste a hipótese de que σ 2 = 0,03 contra a alternativa de que σ 2 ≠ 0,03 para uma amo
Um estudo foi conduzido no Departamento de Medicina Veterinária da Universidade da Virgínia para determinar se a ‘resistência’ de uma ferida causada por uma incisão cirúrgica é afetada pela temperatur
Em um estudo conduzido no Instituto Politécnico e Universidade Estadual da Virgínia, os níveis de ácido ascórbico no plasma de mulheres grávidas foram comparados entre as fumantes e as não-fumantes. T
As notas em um curso de estatística para um semestre em particular são:Teste a hipótese, num nível de significância de 0,05, de que a distribuição das notas é uniforme.
No Exercício 10.41, teste a hipótese, no nível de significância 0,05, de que σ 1 2 = σ 2 2 contra a alternativa σ 1 2 ≠ σ 2 2 e σ 1 2 eσ 2 2 são as variâncias para o número de organismos por metro qua