O Exercício 4 forneceu dados sobre x = o aumento do volume de DBO e y = remoção do volume de DBO. Os valores pertinentes são
a. Obtenha a equação da reta dos mínimos quadrados. b. Preveja o valor da remoção do volume de DBO para uma única observação, feita quando o aumento do volume de DBO é 35, e calcule o valor do resíduo correspondente. c. Calcule a SQE e, em seguida, uma estimativa pontual de . d. Que proporção da variação observada na remoção pode ser explicada pela relação linear aproximada entre as duas variáveis? e. Os dois últimos valores x, 103 e 142, são bem maiores que os outros. Como a equação da reta dos mínimos quadrados e o valor de r2 são afetados pela exclusão das duas observações correspondentes da amostra? Ajuste os valores fornecidos e use o fato de que o novo valor de SQE é 311,79.
Passo 1
Usaremos o seguinte:
Regressão linear é uma equação linear de duas variáveis das quais uma é independente e uma é dependente da outra. Seja X uma variável independente e Y dependente. A equação linear é definida por:
Onde são coeficientes estimados. E a fórmula para calcular esses coeficientes é a seguinte:
Nesta tarefa temos duas amostras com tamanho amostral . Agora os valores necessários para esta amostra são fornecidos abaixo
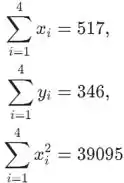
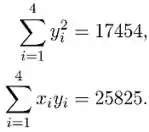
Os dados são fornecidos na tabela a seguir:

- Nesta subseção, precisamos obter a equação da reta de mínimos quadrados. Agora vamos usar a fórmula dada no início desta tarefa e agora precisamos encontrar os valores apropriados. Temos a seguir
- Agora precisamos encontrar a previsão de BOD quando BOD for e então encontraremos o erro de previsão:
- Agora precisamos calcular SSE e então estimar . Temos a seguir
- Agora precisamos encontrar a proporção da variação observada na remoção que pode ser explicada com este modelo. Essa proporção descreve o coeficiente de determinação r², então precisamos encontrar esse valor. Temos a seguir
- Agora vamos repetir o procedimento anterior, vamos repetir excluindo os dois últimos valores. Agora o número de observações é 12 e a tabela com os dados é dada abaixo:

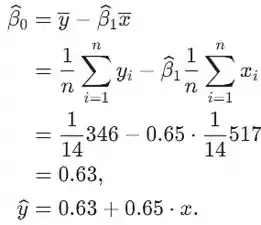
Como podemos ver no cálculo anterior, o modelo de previsão para esses dados é
Passo 2
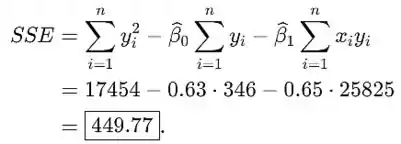
Obtivemos que SSE é 449.77 e agora vamos usar isso para obter a estimativa de da seguinte forma:
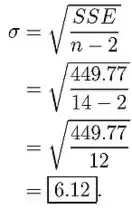
Como podemos ver cerca de 97% desses dados, podemos descrever com este modelo de previsão.

Agora precisamos calcular os valores necessários para repetir a análise sem os dois últimos valores para x e y. Nós seguindo:
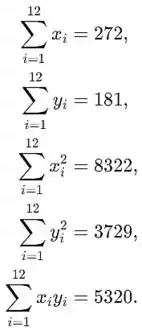
Agora precisamos encontrar os valores médios para esses conjuntos de dados
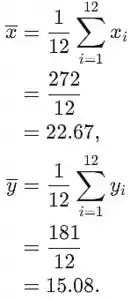
Passo 2
Agora vamos obter a equação da reta de mínimos quadrados. Agora vamos usar a fórmula dada no início desta tarefa e agora precisamos encontrar os valores apropriados. Temos o seguinte:

Agora precisamos calcular SSE e então estimar . Temos a seguir
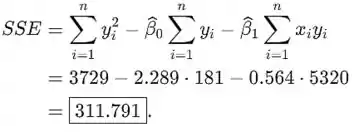
Obtemos que SSE é
Agora vamos usar isso para obter o coeficiente de determinação para ver a proporção de variação observada na remoção que pode ser explicada com este modelo. Temos o seguinte:
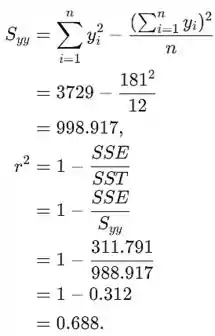
Como podemos ver com este modelo fixo, explicaremos cerca de 69% dos dados
Resposta
Respondemos a todas as perguntas nesta tarefa.