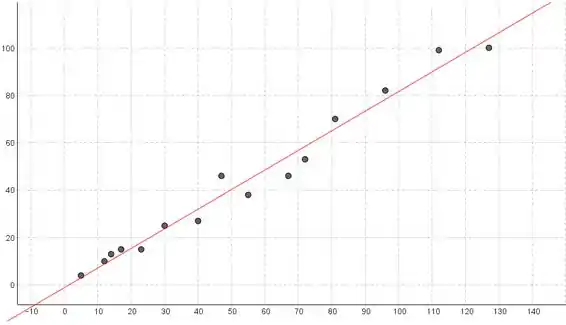
O artigo “Characterization of Highway Runoff in Austin, Texas, Area” (J. of Envir. Engr., 1998, p. 131–137) apresentou um gráfico de dispersão, com a reta dos mínimos quadrados, de x volume de chuva (m3 ) e x volume de runoff [chuva não absorvida pelo solo] (m3 ) de um determinado lugar. Os valores a seguir foram reproduzidos do gráfico
Passo 1
- Encontre e como foi feito na tabela abaixo
- substitua x na equação de regressão por 50 e avalie
-
Determine os valores previstos para todos os dados valores.
Determine a diferença quadrada entre os valores y observados e a média dos valores y.
Determine a diferença quadrada entre os valores y previstos e a média dos valores y.
Determine a diferença quadrada entre os valores y observados e os valores y previstos
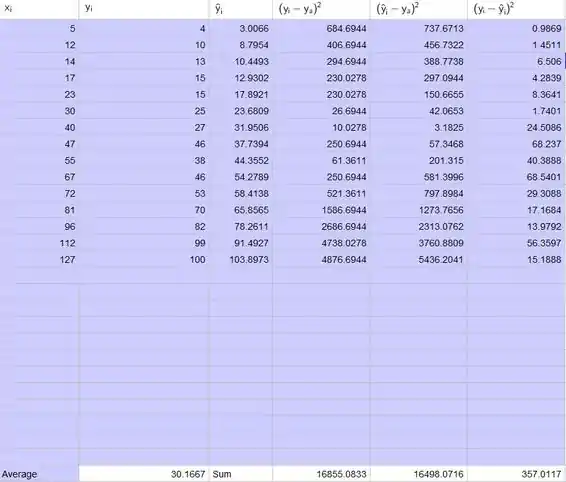
Da tabela temos que:
O desvio padrão do erro é a raiz quadrada da soma dos erros quadrados dividido pelo tamanho da amostra diminuído por 2:
O gráfico de dispersão suporta o uso do modelo de regressão linear simples, porque o gráfico de dispersão não contém curvatura forte e o padrão parece ser aproximadamente linear.
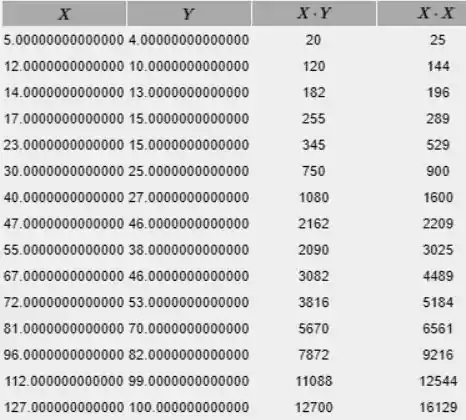
Encontrar a soma de cada coluna
substitua a e b na fórmula da equação de regressão
Assim, a eficiência média real prevista é 40.2204
Passo 2
O coeficiente de determinação é a razão de SSR e SST
Isso significa, então, que 97,53% da variação observada no volume de escoamento pode ser atribuída à relação de regressão linear simples entre as variáveis.
Resposta
- Sim
- 97,53% da variação observada no volume de escoamento pode ser atribuída à relação de regressão linear simples entre as variáveis.