Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 27

Suponha que um investigador tenha dados sobre a quantidade de espaço na prateleira x reservado para expor um determinado produto e a receita de vendas y desse produto. O pesquisador talvez queira ajustar um modelo no qual a reta de regressão real passe por (0, 0). O modelo apropriado é Y 1x . Suponha que (x1, y1), ..., (xn, yn) sejam pares observados por meio desse modelo e derive o estimador dos mínimos quadrados de 1. (Sugestão: escreva a soma dos desvios quadrados como uma função de b1, um valor experimental, e use cálculo para determinar o valor de b1 que minimize essa soma

Passo 1

O problema é encontrar o mínimo da função

que será a estimativa. Usando o cálculo, o resultado pode ser obtido por

Desde

a estimativa dos mínimos quadrados pode ser encontrado na relação

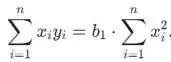
Assim, o estimador de mínimos quadrados é obtido quando você substitui com

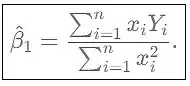
Resposta

Ver o desenvolvimento

Exercícios de Livros Relacionados

Num certo ano, foi feito um levantamento, em n = 10 estados brasileiros, a respeito da renda do estado Y , em milhões de cruzeiros, em função da renda da indústria X 1 e de seviços X 2 (também em milh

Num certo ano, foi feito um levantamento, em n = 10 estados brasileiros, a respeito da renda do estado Y , em milhões de cruzeiros, em função da renda da indústria X 1 e de seviços X 2 (também em milh

Foi feito o levantamento, com n = 12 pessoas, a respeito da idade Y , em função da respectiva altura X 1 (em cm) e do respectivo peso X 2 (em kg).Efetuando os cálculos dos somatórios necessários à mon

Foi feito um levantamento, durante n = 10 meses, a respeito do faturamento total de uma empresa Y , em milhões de cruzeiros, em função do valor das vendas de dois de seus produtos X 1 e X 2 , também e

Num certo ano, foi feito um levantamento, em 10 estados brasileiros, a respeito do número de vagas oferecidas nas escolas de nível superior ( Y ), em 1.000 unidades, em função do número de candidatos