Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 3.Exercícios - Ex. 15
Para os Exercícios 3-15 a 3-18, verifique que as seguintes funções são funções de probabilidade e determine as probabilidade requeridas.
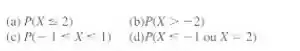
Passo 1
Vamos denotar o intervalo da variável aleatória X como . É dado:
Verifique as condições para a função de massa de probabilidade:
- para cada 1 x. Isso está obviamente cumprido.
Agora, nós simplesmente vamos calcular cada letra:
Passo 2
Letra a:
Passo 3
Letra b:
Passo 4
Letra c:
Passo 5
Letra d:
Resposta
- 1
- 6/8
- 5/8
Exercícios de Livros Relacionados
Rola-se um par de dados honestos. Qual é a probabilidade de o segundo dado sair com um valor maior do que o primeiro?
Os clubes de xadrez de duas escolas são formados por 8 e 9 jogadores, respectivamente. Quatro membros de cada um dos clubes são selecionados aleatoriamente para participar de uma competição entre as d
Um popular jogo de dados é jogado da seguinte maneira: um jogador rola dois dados. Se a soma dos dados é igual a 2 , 3 ou 12, o jogador perde; se a soma é igual a 7 ou 11 , ele vence. Para qualquer re
Um par de dados é rolado até que saia uma soma igual a 5 ou 7. Determine a probabilidade de que um resultado igual a 5 ocorra primeiro. Dica: Suponha que E n represente o evento em que um resultado ig
A cada noite, diferentes metereologistas nos fornecem a “probabilidade” de que irá chover no dia seguinte. Para avaliar o quão boas são estas previsões, é possível atribuir-se escores a cada um desses