Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 101
Um fabricante de semicondutores retira uma amostra aleatória, de tamanho n, de chips, testando-os e classificando-os como defeituosos ou não defeituosos. Faça = 0, se o chip for não defeituoso e = 1, se o cheque for defeituoso. A fração defeituoso da amostra é.
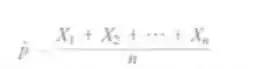
Quais são a distribuição amostral e as estimativas da média amostral e da variância amostral de , quando
- o tamanho da amostra for n=50?
- O tamanho da amostra for n=80?
- O tamanho da amostra for n=100?
- Compare suas respostas para os itens a e c e comente o efeito do tamanho da amostra sobre a variância da distribuição amostral.
Passo 1
Um fabricante de dispositivos semicondutores obtém uma amostra aleatória de tamanho n dos chips e os testa, classificando cada chip como defeituoso ou não defeituoso.
Seja se o chip estiver com defeito e se o chip não estiver com defeito.
A fração da amostra com defeito é
Modelar a ocorrência de defeituosos com a distribuição binomial é geralmente razoável quando o parâmetro binomial p representa a proporção de itens defeituosos produzidos.
Nós sabemos que a distribuição de amostragem de p é aproximadamente normal com média e variância , se p não for muito próximo de 0 ou 1 e se n é relativamente grande.
Portanto...
Passo 2
Letra a:
Para , a média da amostra vai ser:
E a variância da amostra vai ser:
Passo 3
Letra b:
Para , a média da amostra vai ser:
E a variância da amostra vai ser:
Passo 4
Letra c:
Para , a média da amostra vai ser:
E a variância da amostra vai ser:
Passo 5
Letra d:
Das partes a) - c), vemos que a variância da amostra é menor se o tamanho da amostra é maior.
Resposta
- Vemos que a variância da amostra é menor se o tamanho da amostra é maior.