Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 2.Exercícios - Ex. 170
Uma firma de biotecnologia pode produzir kits para testes de diagnósticos, ao custo de US$20,00. Cada kit, do qual há uma demanda na semana de produção, pode ser vendido a US$ 100,00. No entanto, devido à meia-vida dos componentes do kit, o mesmo deve ser jogado fora, caso não seja vendido na semana de produção.
O custo de jogar fora o kit é de US$ 5. A demanda semanal é resumida a seguir:
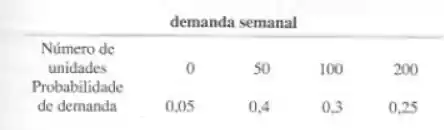
Quantos kits devem ser produzidos a cada semana para maximizar a média de ganhos da firma?
Passo 1
Bom gente, só faz sentido produzir ou kits. Qualquer outro número de kits necessariamente traz mais perdas do que lucro. Por exemplo, se o número de kits produzidos for 57, então no caso que a demanda é 50 ou menos, seria melhor produzir apenas 50 ou menos kits. No caso de demanda superior a 100, seria melhor produzir 100 ou mais kits, porque o lucro excede o preço de produção.
Agora, vamos calcular o lucro nos quatro casos, usando a regra da probabilidade total
e os preços indicados no texto do exercício:
Primeiro, a produção é de 0 kits. Nesse caso, o lucro é 0 também.
Passo 2
Segundo, a produção é de 50 kits.
- A demanda é 0 com probabilidade , portanto, com probabilidade , perdemos o que leva ao lucro médio de
- A demanda é 50 com probabilidade , assim, com probabilidade de , obtemos, o que leva ao lucro médio de
- A demanda é com probabilidade , então, com probabilidade obtemos, o que leva ao lucro médio de
- A demanda é com probabilidade , então com probabilidade , nós obtemos , o que leva ao lucro médio de
- Não importa qual seja a demanda, perdemos para a produção.
- A demanda é 0 com probabilidade , portanto, com probabilidade , perdemos o que leva ao lucro médio de
- A demanda é 50 com probabilidade , assim, com probabilidade de , obtemos, e perdemos o que leva ao lucro médio de
- A demanda é com probabilidade , então, com probabilidade obtemos, o que leva ao lucro médio de
- A demanda é com probabilidade , então com probabilidade , nós obtemos , o que leva ao lucro médio de
- Não importa qual seja a demanda, perdemos para a produção.
- A demanda é 0 com probabilidade , portanto, com probabilidade , perdemos o que leva ao lucro médio de
- A demanda é 50 com probabilidade , assim, com probabilidade de , obtemos, e perdemos o que leva ao lucro médio de
- A demanda é com probabilidade , então, com probabilidade obtemos, e perdemos , o que leva ao lucro médio de
- A demanda é com probabilidade , então com probabilidade , nós obtemos , o que leva ao lucro médio de
- Não importa qual seja a demanda, perdemos para a produção.
No total, o lucro médio é:
Passo 3
Agora, a produção de 100 kits:
No total, o lucro médio é:
Passo 4
Agora, a produção de 200 kits:
No total, o lucro médio é:
Então, vemos que o maior lucro médio é obtido se a produção for de 200.
Resposta
200.