Origem do Termo Regressão. O uso do termo regressão deve-se a Francis Galton, por volta de , quando investigava relações entre características antropométricas de sucessivas gerações. Uma de suas constatações era de que “cada peculiaridade de um homem é transmitida aos seus descendentes, mas, em média, numa intensidade menor”.

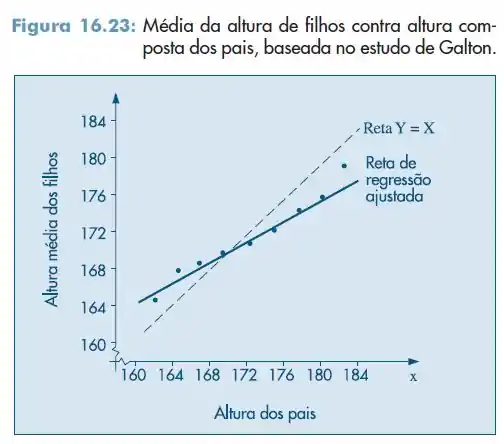
Por exemplo: embora pais com baixa estatura tendam a ter filhos também com baixa estatura, estes têm altura média maior do que a altura média de seus pais. O mesmo ocorre, mas em direção contrária, com pais com estatura alta. Essa afirmação pode ser mais bem compreendida observando-se os dados usados por Galton, e representados parcialmente na Figura . Se as características permanecessem as mesmas de geração para geração, esperar-se-ia que a reta de regressão tivesse seu coeficiente angular próximo de. Em sua análise, Galton encontrou o valor , mostrando que a reta tende para aquela paralela ao eixo e passando pela média A esse fenômeno de a altura dos filhos mover-se em direção à altura média de todos os homens ele chamou de regressão, e às vezes de reversão, tendo aparecido num artigo de , no Journal of the Anthropological Institute, com o título “Regression Towards Mediocrity in Hereditary Stature” — Regressão para a Mediocridade em Estaturas Hereditárias; mediocridade, aqui, referindo-se a média.

Os dados abaixo referem-se a outro experimento de Galton, dentro da mesma investigação,

procurando estudar a relação entre o diâmetro, em centésimos de polegada, de ervilhas-pais e ervilhas-filhas . Analise a reta de regressão para os dados e interprete os coeficientes.

Passo 1

Resposta