Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.2 - Ex. 4b
A função de probabilidade conjunta entre as variáveis aleatórias X e Y é apresentada na próxima tabela.
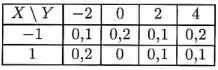
- Obtenha as tabelas marginais de frequência.
- X e Y são independentes?
- Calcule a covariância e a correlação entre X e Y.
Passo 1
- Para que X e Y sejam independentes, teríamos que todas as probabilidades conjuntas devem ser iguais ao produto das correspondentes probabilidades marginais. Vamos verificar se isso é verdade através de um exemplo:
Vamos conferir se .
Passo 2
Se o lado direito e o lado esquerdo da equação não forem em iguais, então as variáveis não são independentes:
Como:
Então as variáveis não são independentes.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
10-29. Considere o experimento da resistencia ao cisalhamento descri-to no Exemplo 10-9.a) Construa, usando os dois métodos. o intervalo de confianca de 9596para a diferença na resisténcia média ao ci
10-33. Quinze homens adultos. entrc as idades de 35 e 50 anos. partici-param de um estudo para avaliar o efeito da dicta e de exercicios no nivelde colestcrol no sangue. O colesterol total foi medido
10-32.Umcientista de computacão está investigando a utilidade de duasditerentes linguagens de programação na melhoria das tarefas compu-tacionais. Dozc programadores experientes. familiarizados com am
Quatro fornos elétricos, que foram derrubados durante o transporte, são inspecionados e classificados como contendo grandes, pequenos ou nenhum defeito. No passado, 60% dos fornos derrubados tinham gr
Uma companhia de marketing realizou uma análise de risco para um fabricante de fibras sintéticas e concluiu que novos competidores não apresentam risco 13% das vezes, risco moderado 72% das vezes e ri