Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 33
10-33. Quinze homens adultos. entrc as idades de 35 e 50 anos. partici-
param de um estudo para avaliar o efeito da dicta e de exercicios no nivel
de colestcrol no sangue. O colesterol total foi medido em cala indivi-
duo inicialmente e depois de trés meses de participaçäo em um progra-
ma de exereicios aerobios e mudanças para uma dieta de baixo teor de
gordura. Os dados são apresentados na tabela a seguir.
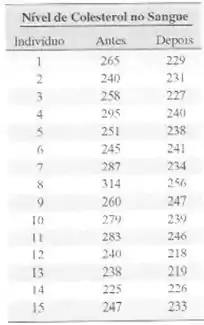
a) Os dados confirmam a afirmação de que dicta com baixo teor de
gordura e um programa de exercicios aeróhios são valiosos para una
redução média nos níveis de coleslerol no sanguc? Use a - 0.05.
Encontre o valor P.
b) Calcule um limite unilatcral de confianca quc pode ser usado para
responder a qucstão do item (a).
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
Tamanho da amostra
Nível de significância
Medidas descritivas
Vamos primeiro determinar a diferença entre cada par de valores de dados:
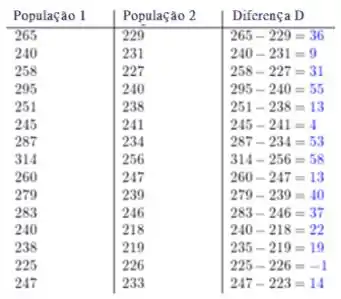
Determine a média da amostra das diferenças. A média é a soma de todos os valores dividida pelo número de valores.
A variância é a soma dos desvios quadrados da média dividido por . O desvio padrão é a raiz quadrada da variância. Determine o desvio padrão da amostra das diferenças:
Passo 2
Letra a:
A afirmação dada é: a diferença média é positiva.
A afirmação é a hipótese nula ou a hipótese alternativa. A hipótese nula afirma que a média da população é igual à mina mencionada na reclamação. Se a hipótese nula for a afirmação, então, a hipótese alternativa afirma o oposto da hipótese nula.
Determine o valor da estatística de teste:
O valor P é a probabilidade de obter o valor da estatística de teste ou um valor mais extremo, assumindo que a hipótese nula é verdadeira. O valor P é o número (ou intervalo) no título da coluna da tabela T-Student no apêndice que contém o valor t na linha .
Se o valor P for menor que o nível de significância então a hipótese nula é rejeitada.
Há evidências suficientes para apoiar a alegação de que a dieta com baixo teor de gordura e os exercícios aeróbicos são valiosos na produção de uma redução média nos níveis de colesterol no sangue. Esses exercícios são importantes na produção de uma redução média nos níveis de colesterol no sangue.
Passo 3
Letra b:
Determine o usando a tabela V com
Os limites inferiores do intervalo de confiança são então:
Resposta
- Há evidências suficientes para apoiar a alegação de que a dieta com baixo teor de gordura e o exercício aeróbio são valiosos na produção de uma redução média dos níveis de colesterol no sangue.