A porcentagem anual média da receita municipal empregada em saneamento básico em pequenos municípios de um estado tem sido (admita que esse índice se comporte segundo um modelo Normal). O governo pretende melhorar esse índice e, para isso, ofereceu alguns incentivos. Para verificar a eficácia dessa atitude, sorteou 10 cidades e observou as porcentagens investidas no último ano. Os resultados foram (em porcentagem):

Os dados trazem evidencia de melhoria, ao nível de ?

Caso altere a média, dê um intervalo de confiança para a nova média.

Beleza, vamos definir o nosso teste de hipótese:

Perceba que queremos testar se houve ou não melhoria, se rejeitarmos então teremos evidências de que o investimento médio em saneamento foi maior, indicando uma melhoria.

Por outro lado se aceitamos não teremos evidências de que ocorreu um aumento nos investimentos.

Top! Agora vamos buscar nossa região crítica, adotando :

Lembrando que teremos uma Rc unilateral superior, pois é a hipótese alternativa quem define isso; portanto se apresenta o sinal de maior a RC pega esse sinal pra ela.

Agora falando sobre a tabela de distribuição de t-student, ela sempre nos da colunas com valores para os quais:

Mas temos:

E como nossa RC é UNILATERAL , então:

É justamente nessa coluna que vamos olhar, e buscar a intersecção dela com a linha de graus de liberdade

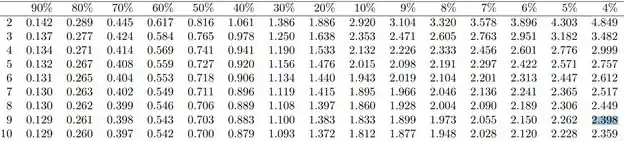
Ou seja:

Etnão nossa RC será:

Por último, vamos realizar o teste sob

Portanto, , devemos REJEITAR .

Com isso, devemos fazer mais uma coisinha, um IC.

Ele tem a seguinte forma:

Dessa vez teremos em vez de , percebeu? Isso porque estamos fazendo um intervalo BILATERAL, e quando isso ocorre:

Então para obter o tal vamos olhar agora na coluna de :

Portanto:

Com isso, encontramos , basta substituir e obter o IC:

E

Percebeu como o não está no intervalo, fato que comprova um aumento no investimento médio em saneamento.