Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 8.Exercícios propostos - Ex. 9
Uma pesquisa de opinião pública numa comunidade mostrou que 46% das pessoas são favoráveis a um projeto de lei. Determinar a probabilidade de que a maioria das pessoas, de um conjunto amostral de 1.000 pessoas, seja favorável a tal projeto.
Passo 1
Oi pessoal. Vamos pensar juntos neste exercício?! Iremos iniciar relembrando de algumas teorias.
Ao retirar uma amostra aleatória de uma população, cada valor da amostra constitui uma variável aleatória cuja distribuição de probabilidades é a mesma da população no instante da retirada desse elemento para a amostra.
A distribuição amostral da proporção é quando temos uma população infinita (), com a probabilidade de sucesso () de um certo evento e de insucesso ().
Se a amostra for suficientemente grande, pode-se aproximar a Binomial por uma Normal de mesma média e mesma variância (na prática, para efeito dessa aproximação devemos considerar: e , ou ainda, para próximo de , se ), isto é:
Pelo enunciado temos os seguintes dados:
- ;
- ;
- .
E queremos saber a probabilidade de que a maioria das pessoas seja favorável ao projeto, ou seja:
Passo 2
Então para :
Pela Tabela da Distribuição normal, temos:
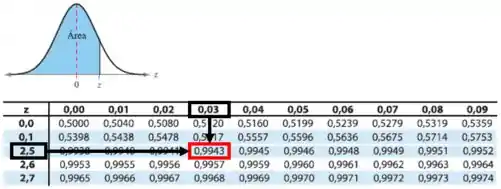
Pela figura presente na tabela:
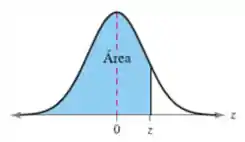
Podemos reparar que o valor obtido é para valores menores que 0,50:
Passo 3
Para valor maior que 0,50:
Então a probabilidade de que a maioria das pessoas seja favorável ao projeto:
Até mais pessoal
Resposta
.