Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 14a

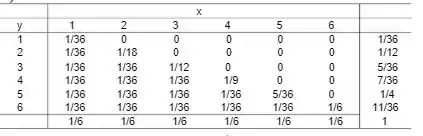
Lançam-se dois dados perfeitos. X indica o número obtido no primeiro dado e Y o maior

ou o número comum nos dois dados. Escreva por meio de uma tabela de dupla entrada a distribuição conjunta de X e Y.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para pegar o que aconteceu lá na combinação dos dados e montar uma tabelinha. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser lembrar como calculamos a probabilidade de um evento acontecer com dois dados.

Mas uma coisa muito importante é que o X tem que ser menor ou igual ao Y. Isso quer dizer que, se o Y for 2, o X só pode ser 1 ou 2, entendeu?? Esse raciocínio segue para todos os números do dado.

Então, só precisamos calcular a probabilidade para cada evento.