Um método usado para distinguir rochas graníticas (G) e basálticas (B) é examinar uma parte do espectro infravermelho da energia solar refletida na superfície da rocha. Sejam as intensidades de espectro medidas em três diferentes comprimentos de onda. Normalmente, para granito, , enquanto para basalto . Quando as medidas são feitas de forma remota (usando aeronaves), podem surgir diversas ordenações de Ri s, se a rocha for basalto ou granito. Voos sobre regiões de composição conhecida resultaram nas seguintes informações:
Suponha que, para uma rocha selecionada aleatoriamente em determinada região, P(granito) 0,25 e P(basalto) = 0,75.
a. Mostre que P(granito |R1
b. Se as medidas forneceram R1
c. Usando as regras de classificação indicadas nas partes (a) e (b), ao selecionar uma rocha dessa região, qual é a probabilidade de uma classificação errada? [Sugestão: G pode ser classificado como B ou B como C e P(B) e P(G) são conhecidos].
d. Se P(granito) = p em vez de 0,25, há valores de p (diferentes de 1) para os quais uma pessoa sempre classificaria uma rocha como granito?
Passo 1
Beleza meus bacanos?! Espero que esteja tudo bem com vocês, vamos dar início a mais uma resolução com o padrão de qualidade do responde aí.
O enunciado da questão nos dá a seguinte tabela
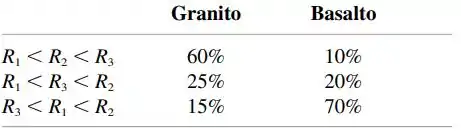

- , então classifique como basalto
- A probabilidade de uma classificação errada é
- Precisamos encontrar tal probabilidade que classifique sempre uma rocha como granito. Então, na verdade, precisamos encontrar pp para o qual
Passo 2
, então classifique como basalto.
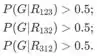
Nestes casos, sempre classificaríamos uma rocha como granito (ver (a) e (b)). Do primeiro temos que
![]()
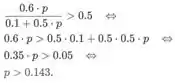
Da mesma forma, para os outros dois,
![]()
![]()
onde, de , o seguinte é verdadeiro

e, de , o seguinte é verdadeiro
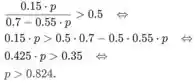
Como todos os três mencionados devem ser satisfeitos, temos que pegar aquele que é o maior, e é p>0,824.
Para concluir, para qualquer p>0,824 uma rocha sempre será classificada como granito.
Resposta
Ver o desenvolvimento