Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 75
Mostre que a seguinte função satisfaz as propriedades de uma função de probabilidade conjunta: determine o seguinte:
Determine o seguinte:
Passo 1
Oi gente, vamos resolver essa questão aqui que é gigante, mas calma, que não é tão difícil quanto parece!
A função de massa de probabilidade de massa conjunta é dada na tabela: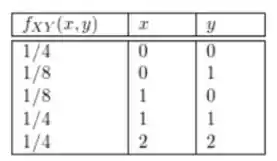
A função de massa de probabilidade da variável aleatória discreta com intervalo satisfaz o seguinte:
O seguinte é válido:
Aqui usamos que para a combinação de x e y de modo que
Isso significa que a função é a função de massa de probabilidade.
Passo 2
Letra a:
Aqui usamos o fato de que, uma vez que e , x tem que ser 0. Da mesma forma para y, pode ser 1 ou 0, que pode ser representado como a união de dois eventos.
A probabilidade de união de eventos disjuntos é a soma das probabilidades dos eventos disjuntos. se A e B são disjuntos.
Passo 3
Letra b:
Passo 4
Letra c:
Passo 5
Letra d:
Mesma coisa acontece na letra a
Passo 6
Letra e:
A expectativa matemática da variável aleatória discreta X é a soma do produto de cada possibilidade na faixa de X com sua probabilidade :
Calculamos a distribuição marginal por definição:
Combinando essas duas equações, temos:
E,
Passo 7
é a variância da variável aleatória X definida como:
Para calcular , observe que é uma variável aleatória discreta e que pode ser escrita como , sabemos que:
Agora calculamos e como:
Você pode o cálculo das probabilidade como uma distribuição marginal.
Agora podemos calcular as variâncias pela definição:
Passo 8
Letra f:
Calculamos as distribuições marginais por definição:
E já explicamos como calculá-lo, então:
Passo 9
Letra g:
Precisamos encontrar a distribuição da variável aleatória . A partir da definição de probabilidade de condicional, temos:
onde são A e B são eventos, e . Para duas variáveis aleatórias X e Y, a distribuição de probabilidade condicional pode ser calculado como:
Portanto, o seguinte é verdadeiro:
Calculando os valores para todos os e obtemos a distribuição. Da tabela da função de massa de probabilidade conjunta, obtemos os valores:
Passo 10
Letra h:
Calculamos pela definição acima:
Passo 11
Letra i:
Para que X e Y sejam independentes, o seguinte tem que ser verdade para todo x, y:
e não é verdade.
Passo 12
Letra j:
A correlação entre as variáveis aleatórias X e Y é definido como:
onde é a variância da variável aleatória X definida como:
e a covariância 'entre as variáveis aleatórias X e Y é
Para calcular ), observe que XY é uma variável aleatória discreta e que pode ser escrito como , então, sabemos que
Disso, calculamos como:
Evitamos aqueles que contêm probabilidade zero ou zero como valor. Usando o que achamos na letra e, temos todos os valores, então podemos calcular:
Resposta
- a função é a função de massa de probabilidade.
- Não são independentes