Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 18
As falhas decorrentes de fadiga de alto ciclo em motores de avião de turbina a gás são um problema que tende a se propagar. O artigo "Effect of Crystal Orientation on Fatigue Failure of Single Crystal Nickel Base Turbine Blade Superalloys (J. of Engineering for Gas Turbines and Power, 2002, p. 161–176) apresentou os dados a seguir e ajustou um modelo de regressão não-linear a fim de prever a amplitude do esforço dos ciclos até a fratura. Ajuste um modelo apropriado, investigue a qualidade desse ajuste e preveja a amplitude quando o número de ciclos até a fratura = 5.000.
Passo 1
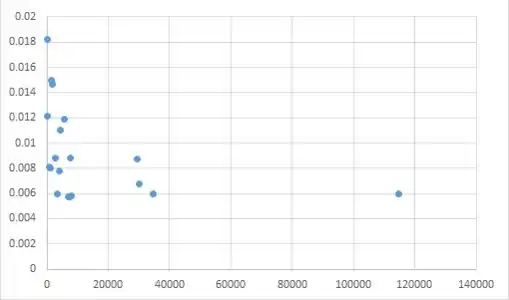
Um modelo apropriado, após verificar os gráficos de dispersão (o que você deve sempre fazer), é
A transformação para linearizar é
e obteria uma forma linear, que pode ser estimada pelo método dos mínimos quadrados
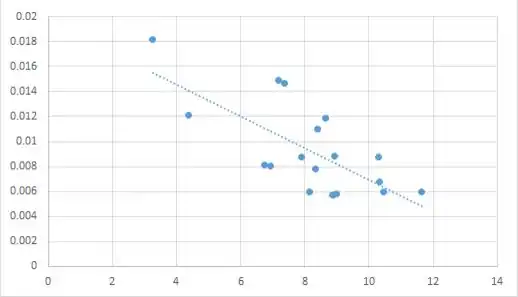
Um gráfico de dispersão de dados transformados sugere um padrão linear; assim, um modelo de regressão linear simples é um bom ajuste.
Passo 2
A estimativa de mínimos quadrados da inclinação no modelo de regressão linear simples é
A estimativa de mínimos quadrados da interceptação é
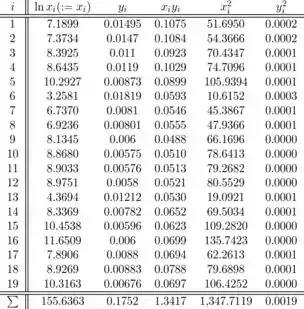
As seguintes somas são necessárias para calcular as estimativas de mínimos quadrados e são fornecidas acima (estes valores são arredondados):
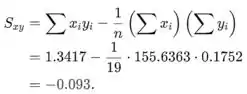
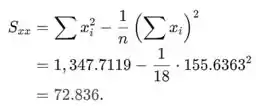
Usando os resultados anteriores
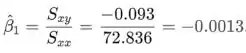
Encontrando usando as somas dadas acima, a estimativa do intercepto é
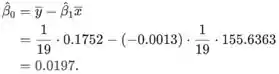
A linha de regressão linear é
Para calcular as estimativas de α e β um modelo deve ser transformado; assim, as estimativas são
Para investigar a qualidade do ajuste, devem ser calculados gráficos residuais, um teste t ou coeficiente de determinação. A maneira mais fácil de investigar a qualidade é testando as hipóteses apropriadas.
Ao testar contra uma das alternativas, o valor da estatística de teste é
Dependendo da hipótese alternativa, o valor P pode ser determinado como área correspondente sob . O teste de utilidade do modelo:
O teste de uso é o teste de utilidade do modelo.
A variância e o desvio padrão do estimador são
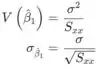
Ao estimar o desvio padrão σ com s você obtém estimativa de
A soma dos quadrados dos erros, SSE, é
A estimativa do desvio padrão σ é
A soma dos quadrados dos erros, SSE, é
A fórmula computacional para SSE é
Pela fórmula computacional, o valor de SSE é
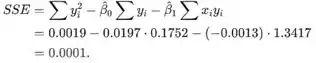
Passo 3
Portanto, a estimativa de σ é
A estimativa do desvio padrão do estimador é
Portanto, o valor da estatística de teste é
O valor PP é a área correspondente sob o curva
que foi calculado por meio de um software. Finalmente, desde
Rejeitar a hipótese nula em determinado nível de significância. O modelo é adequado.
Um intervalo de previsão de 95% para y quando deve ser calculado.
Intervalo de previsão
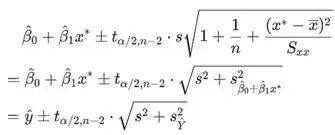
é um intervalo de previsão de para uma observação futura Y, quando .
O valor de quando , usando o modelo de regressão linear simples, é
A variância de uma variável aleatória é
O desvio padrão é a raiz quadrada da expressão. Ao substituir (estimar) σ por s você obtém a estimativa da variância e/ou desvio padrão da variável aleatória .
A estimativa do desvio padrão de é
Os valores necessários para calcular um intervalo de previsão de 95% podem ser encontrados acima; assim, um intervalo de previsão de 95% quando é
Este é um intervalo de previsão de y quando .
Há muitas outras maneiras de ver a validade do ajuste; no entanto, eles não serão apresentados aqui.
Resposta
Transformar para linearizar; Use teste t e gráficos; Calcular intervalo de previsão: (0.0030,0.0146).