Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 10.Problemas - Ex. 5e
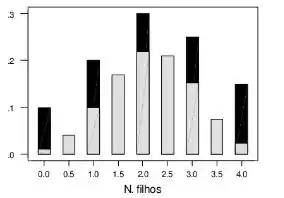
No Problema 3, se X indicar o número de filhos na população, X1 o número de filhos observados na primeira extração e X2 na segunda. Faça num mesmo gráfico os histogramas de X e de Xméd.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para dizer qual a distribuição amostral. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser analisar as probabildades pela tabela.
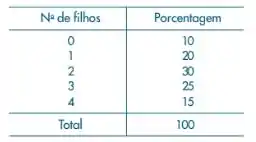
A partir disso, podemos calcular o que ele nos pede.
Passo 3
Pronto!! Agora é só montar o histograma!!
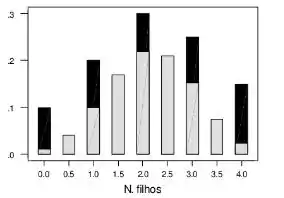
Resposta
Exercícios de Livros Relacionados
Quando o desvio padrão da amostra S se baseia em uma amostra aleatória de uma distribuição normal da população, pode ser demonstrado que E ( S ) = 2 / ( n - 1 ) Γ ( n / 2 ) σ / Γ ( ( n - 1 ) / 2 ) Use
a. Seja X 1 , … , X n a amostra aleatória de uma distribuição uniforme em [ 0 , θ ] Então, a emv de θ é θ ˆ = Y = m a x X i . Use o fato de Y ≤ y se e somente se cada X i ≤ y para encontrar a fdc de Y
A média dos erros quadráticos de um estimador θ ˆ é M S E ( θ ˆ ) = E ( θ ˆ - θ ) 2 . Se θ ˆ é não-tendencioso, então M S E ( θ ˆ ) = V ( θ ˆ ) , mas em geral M S E ( θ ˆ ) = V ( θ ˆ ) + ( desvi
Todos os n espécimes serão pesados duas vezes na mesma escala. Represente por X i e Y i os dois pesos observados do i-ésimo espécime. Suponha que X i e Y i sejam independentes entre si, cada um normal
Um estimador θ é dito ser consistente se para qualquer ϵ ˆ0 , P ( | θ ˆ - θ | ≥ ϵ ) ↔ 0 quando n ↔ ∞ . Isto é, θ ˆ é consistente se, à medida que o tamanho da amostra aumenta, menor é a probabilidade