Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 14.Problemas - Ex. 9
Um produto novo é lançado por uma empresa, e, para verificar a sua aceitação, dois
grupos de pessoas de duas cidades são consultados. De pessoas da cidade ,
gostaram do produto e, de pessoas da cidade , gostaram do produto. Há evidên-
cias que o produto seja igualmente aceito nas duas cidades?
Passo 1
Com base nos dados do exercício, vamos construir tabelas para a frequência observada e para frequência esperada :
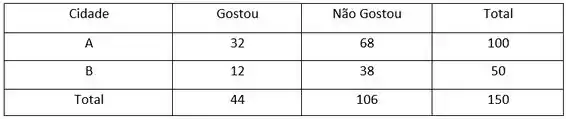
Agora, vamos construir uma tabela para a estatística:
Passo 2
Vamos calcular a estatística do teste:
O valor crítico do teste é .
Resposta
Como , não rejeitamos a hipótese de que o produto seja igualmente aceito nas duas cidades.
Exercícios de Livros Relacionados
( a ) Estabeleça as hipóteses de interesse nesse experimento. ( b ) Teste as hipóteses anteriores e tire conclusões, usando a análise de variância com α = 0,05 . ( c ) Analise graficamente a interação
( a ) Há qualquer indicação de que os fatores afetam a taxa de crescimento da fratura? Há qualquer indicação de interação? Use α = 0,05 ( b ) Analise os residuos desse experimento. ( c ) Repita a anál
( a ) Qualquer evidência confirmando a afirmação de que os níveis do tratamento com polissilício ou das condições de recozimento afetam a corrente? Essas variáveis interagem? Use α = 0,05 ( b ) Analis
( a ) Estabeleça e teste as hipóteses apropriadas usando a análise de variância com α = 0,05 . ( b ) Os resíduos podem ser obtidos de e i j k l = y i j k l = y - i j k l , Analise graficamente os resí
Considere um experimento fatorial com dois fatores. Desenvolva uma fórmula para encontrar um intervalo de confiança de 10 0 1— α % para a diferença entre quaisquer duas médias, tanto para um fator na