Enunciado
Probabilidade e Estatística - Probabilidade, um curso moderno com aplicações, de Sheldon Ross- Ed: 8º - Capítulo 1.Problemas - Ex. 7b
De quantas maneiras diferentes 3 garotos e 3 garotas podem sentar-se em
fila se os garotos e as garotas se sentarem juntos?
Passo 1
Opa galeeeeera! Hoje vamos entender mais um pouco sobre o Princípio Fundamental da Contagem (PFC).
Aqui temos 3 garotos e 3 garotas e há a restrição de que garotos devem estar agrupados, e garotas devem estar agrupados. Então vamos quebrar o problema em 2 partes.
Primeiro vamos descobrir de quantas formas podemos formar cada grupo, e depois quantas formas podemos arranjar estes grupos em uma fila.
Passo 2
Então vamos escolher primeiro como vamos compor o grupo das garotas e depois o dos garotos. Lembrando do princípio fundamental da contagem, toda vez que aparecer um “e” no nosso raciocínio, multiplicaremos as possibilidades de cada um dos casos.
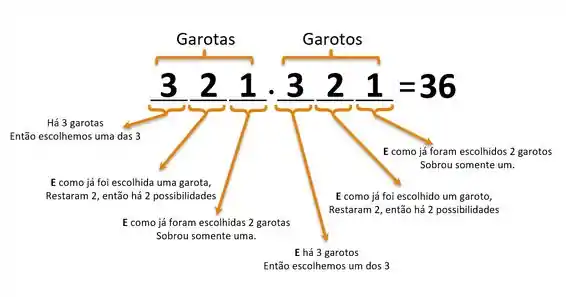
Passo 3
Agora que formamos cada um dos grupos, temos que lembrar que poderiam ser os garotos primeiro e as garotas depois ou o contrário.
Ou seja, há duas formas de mudar as posições de 2 grupos ( ), então multiplicando o nosso caso por 2, teremos casos.
Resposta
3 garotos e 3 garotas podem sentar-se juntos de 72 maneiras diferentes.