Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 12.Problemas - Ex. 32
A receita média, em porcentagem, dos quase 600 municípios de um estado tem sido 7%. O
governo pretende melhorar esse índice e, para isso, está estudando alguns incentivos. Para
verificar os efeitos desses incentivos, sorteou 10 cidades e estudou quais seriam as porcenta-
gens investidas neles. Os resultados foram, em porcentagem, 8, 10, 9, 11, 8, 12, 16, 9, 12, 13.
Admitindo-se que esses números realmente venham a ocorrer, os dados trazem evidência de
melhoria? Caso altere a média do estado, dê um intervalo de confiança para a nova média.
Passo 1
Do enunciado, temos:
X = receita média ( em %) e considerando
e .
N=10 cidades
Temos de realizar o teste da média para uma população com variância desconhecida.
Então:
Devemos calcular a partir das amostras dadas no enunciado:
Passo 2
Teste de hipótese:
Vamos construir a Região Crítica: RC={}
Onde
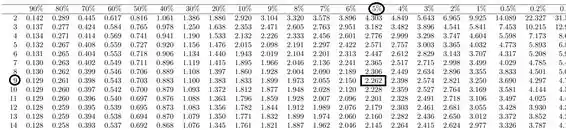
Obs: lembrando que na tabela de distribuição de t-student a porcentagem mostrada é sempre mas como estamos usando o limite unilateral superior(hipótese alternativa), temos
Nossa RC assume a seguinte forma: RC={
Passo 3
Teste sob
Resposta
Como devemos rejeitar e concluímos que existem evidencias de melhoria na receita média das cidades após os incentivos do governo
Intervalo de confiança(
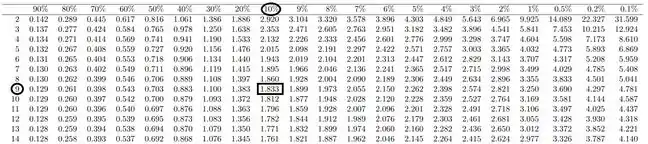
Obs: No intervalo de confiaça temo um limite bilateral com portanto na tabela de t-student:
