Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 9.Exercícios - Ex. 44

Em relação ao Exercício 9.43, determine um intervalo de confiança de 99% para se um pneu de cada marca for atribuído aleatoriamente para cada uma das rodas traseiras de oito táxis e as distâncias, em quilômetros, são as registradas a seguir:

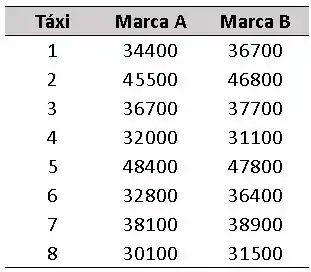
Assuma que as diferenças entre as distâncias têm distribuição aproximadamente normal.

Passo 1

Falaa, meu querido/minha querida. Para um intervalo de confiança para μ 1 - μ 2 , com σ 1 2 ≠ σ 2 2 e ambos desconhecidos, nós temos o intervalo:

( x - 1 - x - 2 ) - t α / 2 σ 1 2 n 1 + σ 2 2 n 2 < μ 1 - μ 2 < ( x - 1 - x - 2 ) + t α / 2 σ 1 2 n 1 + σ 2 2 n 2

Onde, t α / 2 é o valor t com os graus de liberdade definido por:

v = s 1 2 / n 1 + s 2 2 / n 2 2 s 1 2 / n 1 2 / ( n 1 - 1 ) + s 2 2 / n 2 2 / ( n 2 - 1 )

Então, bora para os cálculos!!!

Passo 2

Usando os dados do Exemplo, nós encontramos as seguintes média:

x - 1 = 37250                           x - 2 = 38352,5

Com as médias definidas, podemos usar as fórmulas já conhecidas para encontramos os desvios-padrão a seguir:

s 1 = 6546,75                       s 2 = 6181,06

Pelo o que o enunciado nos deu 9 9 % = 100 1 - α %

1 - α = 0,9 9

α = 0,0 1

Então, agora precisamos calcular o grau de liberdade:

v = 6546,75 2 / 8 + 6181,06 2 / 8 2 6546,75 2 / 8 2 / ( 8 - 1 ) + 6181,06 2 / 8 2 / ( 8 - 1 ) ≈ 13

Sendo assim, o valor de t 0,01 para valor t com 13 graus de liberdade é dado por t 0,0 05 = 3,01 .

Portanto, o intervalo de confiança solicitado é:

μ 1 - μ 2 = 37250 - 38362,5 ± 3,01 6546,75 2 8 + 6181,06 2 8 = - 1112,5 ± 9588,951

Por fim, a estimativa do intervalo de confiança de 99% para a diferença entre as médias da população é:

- 10701,5 < μ 1 - μ 2 < 8476,451

Resposta

- 10701,5 < μ 1 - μ 2 < 8476,451

Exercícios de Livros Relacionados

Um artigo na revista Journal of sports science apresenta resultados de uma investigação do nível de hemoglobina dos jogadores de hóquei no gelo nas olimpíadas do Canadá. Os dados recortados em (g/dl)
Em um estudo, Germination andEmergence o f Broccoli (Germinação e florescimento do brócolis), conduzido pelo Departamento de Horticultura do Instituto Politécnico da Universidade da Virgínia, um pesqu
Um experimento clínico foi realizado para determinar se um tipo de vacinação tem efeito sobre certadoença. Uma amostra de 1.000 ratos foi mantida emum ambiente controlado por um período de um anoe 500
Os dados a seguir representam a duração de dois filmes feitos por duas produtoras.Assuma que as diferenças entre as distâncias têm distribuição aproximadamente normal.