Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 9.Exercícios - Ex. 47

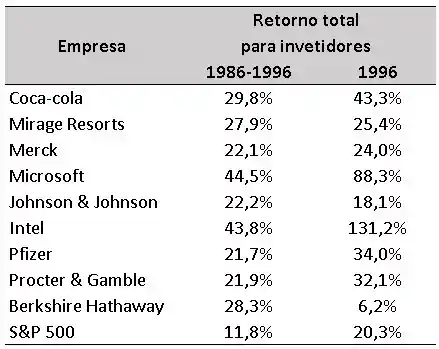
Da revista Fortune (março de 1997), dez de 431 empresas estudadas estão listadas abaixo. Os retornos totais para os dez anos anteriores a 1996, incluindo 1996, estão listados. Determine o intervalo de confiança de 95% para a mudança média na porcentagem dos retornos para os investidores.

Passo 1

Falaa, meu querido/minha querida. Usando o teorema do intervalo de confiança, nós temos a seguinte fórmula

d - - t α / 2 s d n < μ D < d - + t α / 2 s d n

Onde, t α / 2 é o valor t com os graus de liberdade definido por v = n - 1 = 9

Então, bora para os cálculos!!!

Passo 2

Usando os dados do Exemplo, primeiro precisamos encontrar os valores de d , que é o retorno total de 1986-1996 diminuído do retorno total de 1996.

d 1 = 29,8 - 43,3

E assim, sucessivamente até d 10 , depois calculamos a média e encontramos d - = 14,89 .

Com as médias definidas, podemos usar as fórmulas já conhecidas para encontramos o desvio-padrão a seguir:

s d = 30,48

Pelo o que o enunciado nos deu 9 5 % = 100 1 - α %

1 - α = 0,9 5

α = 0 , 05

Sendo assim, o valor de t 0,0 25 para valor t com 9 graus de liberdade é dado por t 0,0 2 5 = 2,262 .

Portanto, o intervalo de confiança solicitado é:

d - - t α / 2 s d n < μ D < d - + t α / 2 s d n

14,89 - 2,262 30,48 10 < μ D < 14,89 + 2,262 30,48 10

Por fim, a estimativa do intervalo de confiança de 95% para a diferença entre as médias da população é:

- 6,92 < μ D < 36,70

Resposta

- 6,92 < μ D < 36,70

Exercícios de Livros Relacionados

Um artigo na revista medicine and science in sports and exercise “electrostimulation training effects on the physical performance of ice hockey players “ - efeitos do treinamento de eletroesimulação n
Em um lote de um processo químico, dois catalisadores foram comparados em relação a seu efeito no resultado do processo de reação. Uma amostra de 12 lotesfoi preparada usando o catalisador 1 e outra a
Um estudo foi conduzido para determinar se certo tratamento em metal tem algum efeito sobre a quantidade de metal removida durante uma operação de decapagem com ácido. Uma amostra aleatória de 100 peç
Dois tipos de roscas são comparados por sua resistência. Cinquenta peças de cada tipo de rosca são testadas sob condições similares. A marca A tem uma resistência à tensão com média de 78,3 quilograma