Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 79

Um dado é jogado 180 vezes com os seguintes resultados:

Esse dado é balanceado? Use um nível de significância de 0,01.

Passo 1

Selvaaaaaaaaaa galerinha, isso mesmo selva haha, tudo certinho??

“Hulk esmaga”, Bora esmagar essa questãozinha comigo?

Testar

H 0 : O   d a d o   e s t á   e q u i l i b r a d o

H 1 : O   d a d o   n ã o   e s t á   b a l a n c e a d o

H 0 : A   d i s t r i b u i ç ã o   d o s   r e s u l t a d o s   é   a   d i s t r i b u i ç ã o   u n i f o r m e   d i s c r e t a

H 1 : A   d i s t r i b u i ç ã o   d o s   r e s u l t a d o s   n ã o   é   u n i f o r m e

O nível de significância dado é de α = 0.01

A estatística de teste é

x 2 = ∑ i = 1 6 f i - e i 2 e i

f i   e   e i representam as frequências observadas e esperadas respectivamente, para a célula ou classe

x 2 distribuição com 6 - 1 = 5 graus de liberdade.

A região critica é x o b s e r v a d a 2 > x 0.01 ; 5 2 onde x 0.01 ; 5 2   está o ponto 0.001 superior da distribuição com 5 graus de liberdade.

Passo 2

Vamos denotar os resultados do lançamento de um dado

Considerando a tabela a seguir

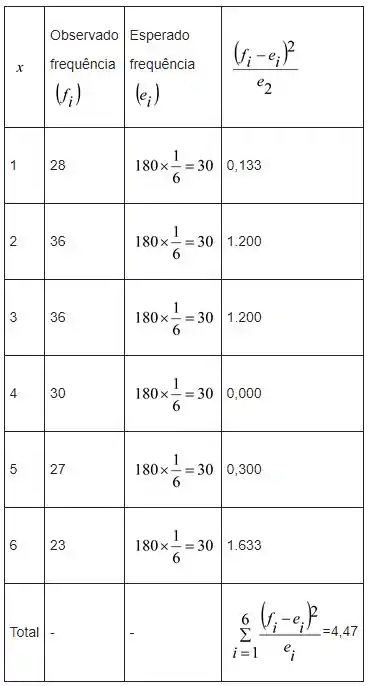
Passo 3

Conseqüentemente, x o b s e r v e d o 2 = 4.47

O valor tabelado de x 0.01 ; 5 2 e 15.086 .

Nosso valor observado x 2 é inferior ao tabelado de x 0.01 ; 5 2 .

Portanto, falhamos em rejeitar a hipótese nula e calculamos que não há evidências suficientes de que a moeda esteja desbalanceada.

“OK, isso foi legal.”

Resposta

Resposta nos passos.

Exercícios de Livros Relacionados

Em um estudo conduzido no Instituto Politécnico e Universidade Estadual da Virgínia, os níveis de ácido ascórbico no plasma de mulheres grávidas foram comparados entre as fumantes e as não-fumantes. T
As notas em um curso de estatística para um semestre em particular são:Teste a hipótese, num nível de significância de 0,05, de que a distribuição das notas é uniforme.
No Exercício 10.41, teste a hipótese, no nível de significância 0,05, de que σ 1 2 = σ 2 2 contra a alternativa σ 1 2 ≠ σ 2 2 e σ 1 2 eσ 2 2 são as variâncias para o número de organismos por metro qua
Um experimento foi conduzido para comparar os conteúdos de álcool em um molho de soja em duas linhas de produção diferentes. A produção foi monitorada oito vezes por dia. Os dados são mostrados a segu
Uma máquina deveria misturar amendoins, avelãs, castanhas de caju e nozes em uma razão de 5:2:2:1. Uma lata com 500 dessas frutas secas misturadas contém 269 amendoins, 112 avelãs, 74 castanhas de caj