Um restaurante popular apresenta apenas dois tipos de refeições: salada completa ou um prato à base de carne. Considere que 20% dos fregueses do sexo masculino preferem a salada, 30% das mulheres escolhem carne, 75% dos fregueses são homens e os seguintes eventos:
H: freguês é homemA: freguês prefere salada
M: freguês é mulherB: freguês prefere carne
Calcular:
Passo 1
Primeiro, vamos “traduzir” os dados do enunciado em evento:
“20% dos fregueses do sexo masculino preferem salada” isso nos diz que o evento A|H tem probabilidade Observe então, que , ou seja 80% dos homens preferem carne.
De modo análogo, “30% das mulheres escolhem carne” isso nos diz que o evento tem probabilidade
“75% dos fregueses são homens” nos diz que o evento tem
Passo 2
Para facilitar, vamos colocar os dados em uma tabelinha e, completá-la usando as seguintes propriedades:
Se , então Isso quer dizer que a probabilidade da intersecção dos eventos “cliente prefere salada” com “cliente é homem” tem probabilidade igual a .
. Logo a probabilidade de um cliente preferir salada é de 32,5%.
Montando a tabela...
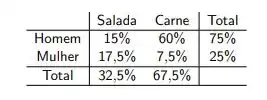
Basta agora olharmos a tabela e resolver as alternativas.
Passo 3
.
.
.
Resposta