Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 14.Exercícios propostos - Ex. 7c
Segundo dados da CESP, foi feito um levantamento, em cidades do estado de São Paulo, a respeito da extensão da rede de transmissão urbana (em km de rede), em função da população economicamente ativa vinculada a atividades urbanas (em mil habitantes) e em função também da extensão territorial da cidade (em km2).
Efetuados os cálculos dos somatórios necessários à montagem de regressão, obtivemos:
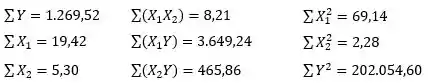
Pede-se:
- Interpretar os valores dos parâmetros da regressão múltipla.
Passo 1
Olá galerinha, tudo bem com vocês? Vem comigo!
A regressão linear múltipla é a regressão em que sabemos como variáveis contribuem para a realização do fenômeno, e a parte funcional da regressão é uma função linear. Onde a estimativa da equação de regressão é dada por:
Onde as estimativas , , , , dos coeficientes , , , , podem ser calculadas pelo método dos mínimos quadrados, partindo de hipóteses análogas aquelas adotadas pela regressão linear simples.
Para o caso de ter apenas duas variáveis explicativas:
Para encontrarmos os valores de , e , iremos utilizar as equações:
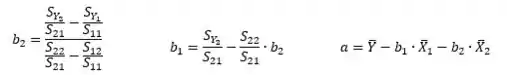
O cálculo das médias (, e ) são dadas pelas seguintes equações:
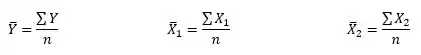
Para as variâncias vamos usar as equações:
E para as covariâncias:
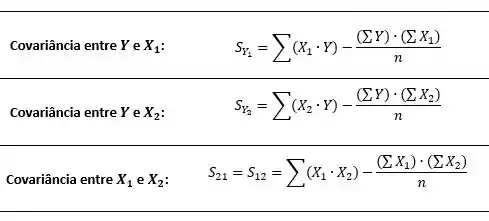
Passo 2
Primeiramente iremos calcular as médias de , e , respectivamente:
O cálculo das variâncias:
E das covariâncias:
Passo 3
Com esses valores, finalmente conseguimos calcular os valores de , e :
Pelo enunciado sabemos que:
- extensão da rede de transmissão urbana (em km de rede);
- população economicamente ativa vinculada a atividades urbanas (em mil habitantes);
- extensão territorial da cidade (em km2).
Então, temos o seguinte:
- é a extensão fixa de rede (em km);
- acréscimo da extensão da rede para cada 1000 habitantes (em km);
- decréscimo da extensão da rede para cada km2 da extensão territorial (em km2).
Espero ter conseguido te ajudar, até mais!
Resposta
Resposta no Passo 3.