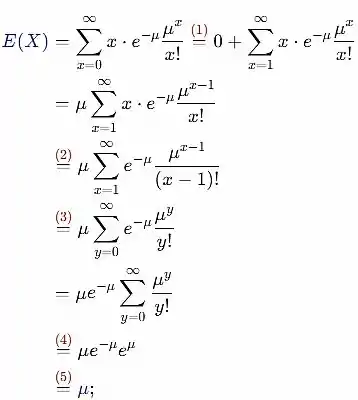Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 3.Exercícios - Ex. 86
Seja X uma distribuição de Poisson com parâmetro . Demonstre que E(X) diretamente da definição de valor esperado. (Sugestão: O primeiro termo da soma é igual a 0, então x pode ser cancelado. Fatore e mostre que o restante soma 1.)
Passo 1
O Valor Esperado (valor médio) de uma variável aleatória discreta X com conjunto de valores possíveis S e pmf p(x) é
Uma variável aleatória X com pmf
para x=0,1,…, é dito ter Poisson Distribution com parâmetro
Passo 2
Portanto, pela definição, o seguinte é verdadeiro
Resposta
Exercícios de Livros Relacionados
Uma rede congestionada de computadores tem 1% de chance de perder um bloco de dados e perdas de blocos são eventos independentes. Uma mensagem de e-mail requer 100 blocos. Qual é a distribuição de blo
Seja X o número de bits recebidos com erro em um canal digital de comunicação e considere que X seja uma variável aleatória binomial, por p = 0.001 . Se 1000 bits forem transmitidos, determine o segui
Considere que o número de erros ao longo de uma superfície magnética gravadora seja uma variável aleatória de Poisson, com uma média de um erro a cada 1 0 5 bits. Um setor de dados consiste em 4096 by
A probabilidade de uma águia matar um coelho em um dia de caça e 10%. Considere que resultados sejam independentes entre dias. Qual é a distribuição do número de dias até que a caça ao coelho tenha su
Um técnico de instalação de um sistema especializado de comunicação enviado para uma cidade somente quando existirem três ou mais ordem de serviço. Suponha que esse serviço sigam a distribuição de Poi