Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 3.Exercícios - Ex. 89
- Em um processo de Poisson, o que deve acontecer no intervalo de tempo (0,t) e no intervalo (t, t+ para que nenhum evento ocorra em todo o intervalo (0, t+ Use esta Hipótese e as Hipóteses 1-3 para escrever a relação entre e .
- Use o resultado da parte (a) para escrever uma expressão por e considere que para obter uma equação envolvendo , derivada de em relação a t.
- Verifique se satisfaz à equação da parte (b)
- Pode-se demonstrar de forma similar às partes (a) e (b) que as Pk(t) devem satisfazer ao sistema de equações diferenciais
Passo 1
- Nenhum evento em (0, t+t) se e somente se nenhum evento em (o, t) e nenhum evento em (t, t+t). Assim, (t+t) = ×P(sem eventos em (t, t+t))
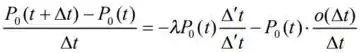
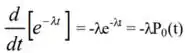
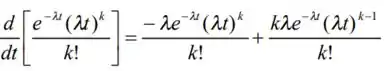
= [1 – t – o(t)]
Passo 2
Passo 3
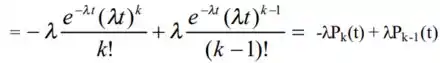
Resposta
Ver o desenvolvimento
Exercícios de Livros Relacionados
De 500 consumidores, uma grande fabricante de aparelhos eletrônicos selecionará aleatoriamente uma amostra sem reposição. Acompanhe estima que 25% dos consumidores forneceram dados úteis. Se a sistemá
Mensagens chegam ao servidor de computadores, de acordo com a distribuição de Poisson, com uma taxa média de 10/h. Determine o tamanho de um intervalo de tempo, tal que 0.90 seja a probabilidade de ne
Um carregamento de compostos químicos chega aqui em 15 depósitos. Três deles são selecionados ao acaso e sem reposição para uma inspeção de pureza. Se dois dos depósitos não satisfizerem os requerimen
Seja a variável aleatória X igualmente provável de ter valores iguais a ⅛, ¼ e ⅜. Determine a média e a variância de X.
A variável aleatória X tem a seguinte distribuição de probabilidade. Determine o seguinte: P ( X ≤ 3 ) P ( X2.5 ) P ( 2.7X5.1 ) E ( X ) V ( X )