Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 7a
suponha que o peso de recém-nascidos (em kg) pode ser considerado uma
variável aleatória com a seguinte densidade:
Qual a probabilidade de, escolhendo ao acaso uma criança, ela ter peso:
- Inferior a kg?
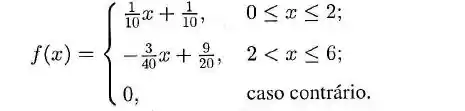
Passo 1
Eai,tudo bem? Bora resolver mais um exercício?
O exercício nos pede para calcular a probabilidade de escolhendo uma criança ao acaso, ela ter preso inferior a três quilos.
Você se lembra desse conteúdo? Se não, é hora de dar aquela revisão. Ok?
Lembrando que é uma função definida por partes.
Passo 2
Assim,
Resposta
Logo,
Exercícios de Livros Relacionados
Uma variável X tem a seguinte função densidade: f x = x - 1 p a r a 1 ≤ x ≤ 2 3 - x p a r a2 ≤ x3 0 p a r ao u t r o sv a l o r e s Pede:a) elaborar o gráfico da função densidade;b) quais são o valor
Sabendo que a função distribuição de uma variável X é: F x = 0 p a r ax ≤ 0 F x = x 2 p a r a0x ≤ 1 2 F x = 1 - 3 1 - x 2 p a r a1 2x1 F x = 1p a r a x ≥ 1 Achar a função densidade de X , calcular a m
O tempo de vida, em horas, de um dispositivo, é dado pela função densidade f t = 1 50.e - ( t 50 ) , t ≥ 0 a) qual q probabilidade de que um desses dispositivos dure mais que 25 e menos que 75 horas?b
Diz-se que um arranjo retangular de mn números organizado em n linhas e m colunas contém um ponto de sela se houver um número que é ao mesmo tempo o mínimo de sua linha e o máximo de sua coluna. Por e
Obtenha a Equação (6.2) calculando a derivada da Equação (6.4).