Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 81

Suponha que X e Y sejam variáveis aleatórias contínuas uniformes e independentes para 0 < x < 1     e 0 < y < 1 . Use a função densidade de probabilidade conjunta para determinar a probabilidade de | X - Y | < 0.5

Passo 1

Sejam X e Y variáveis ​​aleatórias uniformes contínuas e independentes para 0 < x < 1     e 0 < y < 1 .

Vamos encontrar a probabilidade de que | X - Y | < 0.5

Vamos supor que Z = X - Y e V = Y

Para distribuição conjunta, a transformação jacobina é

= 1

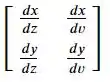
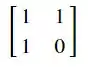
Passo 2

A função de densidade de probabilidade conjunta de Z é:

g ( Z ) = ∫ 0 1 - z ∫ u 1 f ( x , y )

g ( z ) = 1 + z ,   - 1 < z < 0

g ( z ) = 1 - z ,   0 < z < 1

Portanto, a probabilidade de que | X - Y | < 0.5 é:

P ( | Z | < 0.5 ) = P ( - 0.5 < z < 0.5 )

= z - z 2 2 0 0.5 - z + z 2 2 1 0.5

= 0.75

Resposta

P ( | X - Y | < 0.5 ) = 0.75

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a função de probabilidade conjunto de variáveis aleatórias contínuas X e Y seja constante no retângulo. Mostre que X e Y são independente.
Suponha que a faixa das variáveis contínuas X e Y seja. Suponha também que a função densidade de probabilidade conjunta, em que é uma função somente de X e seja uma funções de Y. Mostre que X e Y são
Os tempos de vida de seis componentes principais em uma copiadora são variáveis aleatórias exponenciais e independentes, com médias de 8000 horas, 10000 horas, 10000 horas, 20000 horas, 20000 horas e
A distribuição conjunta das variáveis aleatórias contínuas X, Y e Z é constante ao longo da região x 2 + y 2 ≤ 1 ,0z4 . Determine o seguinte: P ( X 2 + Y 2 ≤ 0.5 ) P ( X 2 + Y 2 ≤ 0.5 , Z2 ) A função