Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 19
Testes de resistência térmica foram executados para investigar a relação entre a temperatura e o tempo de vida de fios esmaltados de poliéster (“Thermal Endurance of Polyester Enameled Wires Using Twisted Wire Specimens”, IEEE Trans. Insulation, 1965, p. 38–44), gerando os dados a seguir.
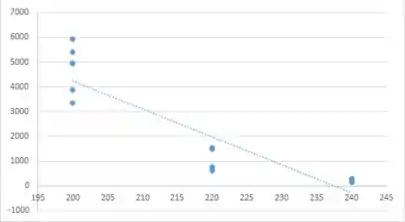
a. Um gráfico de dispersão dos dados sugere uma relação probabilística linear entre o tempo de vida e a temperatura? b. Que modelo é sugerido por uma relação linear entre os valores esperados do ln(tempo de vida) e 1/temperatura? Um gráfico de dispersão dos dados transformados parece consistente com a relação? c. Estime os parâmetros do modelo sugerido no item (b). Que tempo de vida seria previsto para uma temperatura de 220? d. Pelo fato de haver múltiplas observações em cada valor x, o método do Exercício 14 pode ser usado para testar a hipótese nula que expressa que o modelo sugerido no item (b) é correto. Execute um teste no nível 0,01
Passo 1
- Não, o gráfico de dispersão não sugere relação linear entre as variáveis - também não há curvatura.
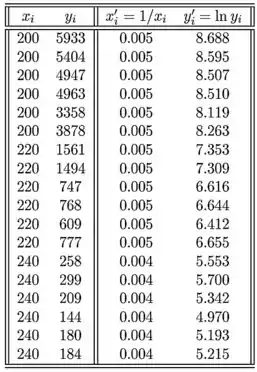
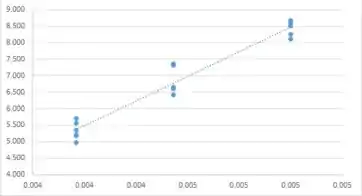
- A tabela a seguir representa os dados transformados e o gráfico de dispersão fornecido sugere linearidade entre as variáveis. Um modelo apropriado para tais dados seria
- Estime α e β no modelo usando o método dos mínimos quadrados.
- Leia atentamente a explicação do exercício! Os valores x são repetidos da seguinte forma:
Um teria o modelo transformado
Onde
A estimativa de mínimos quadrados da inclinação no modelo de regressão linear simples é
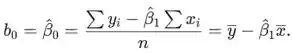
Passo 2
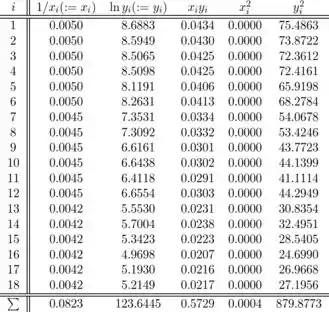
Todos os valores são arredondados!
As seguintes somas são necessárias para calcular as estimativas de mínimos quadrados e são fornecidas acima (estes valores são arredondados):
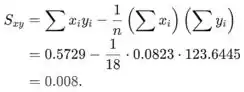
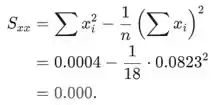
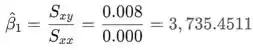
Encontrando usando as somas dadas acima, a estimativa do intercepto é
Para calcular as estimativas de α e β um modelo deve ser transformado; entretanto, α e β no modelo são dados como as estimativas de mínimos quadrados; assim, as estimativas são
Seja agora . Usando o modelo dado acima para predizermos o tempo de vida.
Agora iremos predizer para
Assim, a previsão da vida útil é
Passo 3
6 observações para
Ou igualmente
6 observações para
Médias:
Além disso, o primeiro termo em SSPE, a soma, é
A soma dos quadrados dos erros, SSE, é
A fórmula computacional para SSE é
O valor de SSLFSSLF pode ser calculado usando a fórmula dada no exercício
Com dado , o valor F pode ser encontrado na tabela no apêndice do livro
Com o nível de significância
Por conta disso
Não rejeitamos a hipótese nula nesse nível de significância. Um modelo linear é apropriado.
Resposta
Ver a resolução