Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 22
Três cartas são retiradas, sucessivamente, de um baralho sem reposição. Determine a distribuição de probabilidade para o número de espadas.
Passo 1
Falaa, meu querido/minha querida. Seja a variável aleatória que representa o número de espadas entre as 3 cartas retiradas.
Vamos definir o número de maneiras que podemos retirar as 3 cartas.
As cartas não são repostas. Logo, na primeira carta retirada são 52 cartas no baralho, na segunda 51 e na última carta 51. Então, o número total de maneiras é:
Então, bora para os cálculos!!!
Passo 2
Primeiro, vamos determinar o número de maneiras para retirarmos 3 cartas, sem ser nenhuma de espada.
Sendo assim, a probabilidade de não retirar nenhuma de espadas é:
Passo 3
Agora, vamos definir o número de maneiras de tirar 1 carta de espadas e 2 de qualquer outro naipe.
A carta de espadas pode ser retirada em qualquer uma das 3 cartas, sendo qualquer uma das 13 cartas de espadas.
E as outras duas cartas não de espadas, são 39 e depois 38, como não são repostas. Portanto, o número de maneiras é:
Logo, a probabilidade de tirar duas cartas de espadas e uma de outro naipe é:
Passo 4
Definindo o número de maneiras de tirarmos duas de espadas e uma de outro naipe.
Para a carta que não é de espadas, ela pode ser retirada em qualquer uma das 3 cartas e são 39 cartas.
Nas cartas de espadas, na primeira carta retirada do naipe são 13 cartas e na segunda 12.
Portanto, a probabilidade é:
Passo 5
Por fim, o número de maneiras de retirar as 3 cartas do mesmo naipe.
Nós temos que as 3 cartas serão de espadas, na primeira carta são 13 cartas de espadas no baralho, na segunda 12 e na terceira 11.
Sendo assim, a probabilidade é:
Passo 6
Como vimos nos cálculos acima a distribuição de probabilidade é:
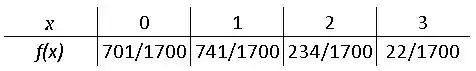
Resposta
Resolução nos passos anteriores.