Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 13

A distribuição de probabilidade de X, o número de imperfeições a cada dez metros de um tecido sintético produzido em rolos contínuos de largura uniforme, é dada por:

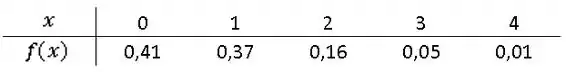
Construa a função de distribuição acumulada de X .

Passo 1

Falaa, meu querido/minha querida. Neste caso, nos foi dada a probabilidade para cada número de imperfeições. Então, para calcularmos a probabilidade acumulada, precisamos fazer a soma das probabilidades anteriores. A definição da função de distribuição acumulada é:

F x = P ( X ≤ x )

Então, bora para os cálculos!!!

Passo 2

Para F ( 0 ) , usando os valores da tabela, encontramos:

F 0 = P ( X ≤ 0 )

F 0 = P ( X = 0 )

F 0 = 0,41

Para F ( 1 ) , usando os valores da tabela, encontramos:

F 1 = P ( X ≤ 1 )

F 1 = P X = 0 + P ( X = 1 )

F 1 = 0,41 + 0,37 = 0,78

Para F ( 2 ) , usando os valores da tabela, encontramos:

F 2 = P ( X ≤ 2 )

F 2 = P X = 0 + P X = 1 + P ( X = 2 )

F 0 = 0 , 41 + 0,37 + 0,16 = 0,94

Para F ( 3 ) , usando os valores da tabela, encontramos:

F 0 = P ( X ≤ 3 )

F 0 = P X = 0 + P X = 1 + P X = 2 + P ( X = 3 )

F 0 = 0,41 + 0,37 + 0,16 + 0,05 = 0,99

Para F ( 4 ) , usando os valores da tabela, encontramos:

F 4 = P ( X ≤ 4 )

F 4 = P X = 0 + P X = 1 + P X = 2 + P X = 3 + P ( X = 4 )

F 4 = 0,41 + 0,37 + 0,16 + 0,05 + 0,01 = 1

Encontramos que a probabilidade acumulada F ( 4 ) é igual a 1. Logo, podemos concluir que cobrimos todo o espaço amostral no cálculo.

Passo 3

Por fim, a função de distribuição acumulada para a variável aleatória X é:

F ( x ) = 0 ,                                         x < 0 0,41 ,             0 ≤ x < 1 0 , 78 ,             1 ≤ x < 2 0 , 94 ,             2 ≤ x < 3 0 , 99 ,             3 ≤ x < 4 1 ,                                         x ≥ 4

Resposta

F ( x ) = 0 ,                                         x < 0 0,41 ,             0 ≤ x < 1 0,78 ,             1 ≤ x < 2 0,94 ,             2 ≤ x < 3 0,99 ,             3 ≤ x < 4 1 ,                                         x ≥ 4

Exercícios de Livros Relacionados

A espessura (em polegadas) de um painel de madeira que um consumidor requer é uma variável aleatória, com a seguinte função de distribuição cumulativa: F ( x ) = 0 ,s ex1 / 8 F ( x ) = 0.2 ,s e1 / 8 ≤
Erros em um canal experimental de transmissão são encontrados quando a transmissão é verificada por um certificador que detecta pulsos que faltam. O número encontrado de erros em um byte de 8 bits é u
Determine a função de distribuição cumulativa da variável aleatória do Exercício 3-24.
Determine a função de distribuição cumulativa da variável aleatória do Exercício 3-23.
Determine a função de distribuição cumulativa da variável aleatória do Exercício 3-14