Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 3.4 - Ex. 6

Uma variável aleatória X tem a seguinte função de distribuição:

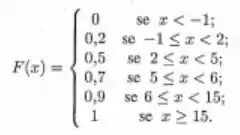
Determine:

  1. A função de probabilidade de X .
  2. P X ≤ 2 .
  3. P X < 2 .
  4. P 3 ≤ X ≤ 12
  5. P X > 14 .

Passo 1

Vamos montar a tabela da função de distribuição, levando em conta que:

P X = x i = F x i - F ( x i - )

Onde F ( x i - ) é o salto que ela deu no ultimo ponto.

Passo 2

  1. Vamos ver como funciona:

    2. P X = - 1 = F - 1 - 0 = 0,2 - 0 = 0,2

    P X = 2 = F 2 - F - 1 = 0,5 - 0,2 = 0,3

    P X = 5 = F 5 - F 2 = 0,7 - 0,5 = 0,2

    P X = 6 = F 6 - F 5 = 0,9 - 0,7 = 0,2

    P X = 15 = F 15 - F 6 = 1 - 0,9 = 0,1

    Perceba que por ser uma função de distribuição, para calcular a função de probabilidade é necessário calcular os saltos que ela da a cada acumulo, e foi isso que fizemos.

    Passo 3

    3. P X ≤ 2 = P X = - 1 + P X = 2 = 0,2 + 0,3 = 0,5

    Passo 4

    4. P X < 2 = P X = - 1 = 0,2

    Passo 5

    5. P X ≤ 3 ≤ 12 = P X = 5 + P X = 6 = 0,2 + 0,2 = 0,4

    Passo 6

P X > 14 = P X = 15 = 0,1

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No Exemplo 1d, calcule a probabilidade condicional de que ganhemos i reais, dado que ganhemos algo; calcule-a para i = 0,1,2,3.
A distribuição de probabilidade da variável aleatória discreta X é f x = 3 x 1 4 x 3 4 3 - x ,x = 0,1 , 2,3 . Determine a média de X.
Em uma floresta vivem 20 renas, das quais 5 são capturadas, marcadas e então soltas. Certo tempo depois, 4 das renas são capturadas. Qual é a probabilidade de que 2 dessas 4 renas tenham sido marcadas
Duas cartas são escolhidas aleatoriamente de um baralho de 52 cartas. Qual é a probabilidade de(a) ambas serem ases?(b) ambas terem o mesmo valor?
Existem n meias em uma gaveta, 3 das quais são vermelhas. Qual é o valor de n se a probabilidade de que duas meias vermelhas sejam retiradas aleatoriamente da gaveta é igual a 1 / 2 ?