Um vendedor de equipamento pesado pode visitar, num dia, um ou dois clientes, com probabilidade de 1/3 ou 2/3, respectivamente. De cada contato, pode resultar a venda de um equipamento por $50.000,00 (com probabilidade 1/10) ou nenhuma venda (com probabilidade 9/10). Indicando por Y o valor total de vendas diárias desse vendedor, escreva a função de probabilidade de Y e calcule o valor total esperado de vendas diárias.
Passo 1
Vamos lá! Para escrevermos a função de probabilidade de Y precisamos das probabilidades de todos os possíveis resultados desse vendedor. Para isso seguindo os dados do enunciado montaremos um diagrama de árvore:
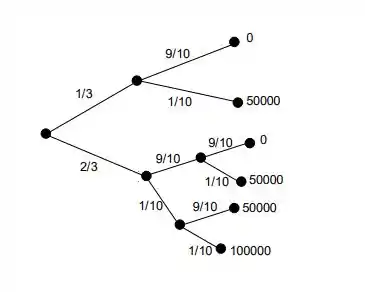
Note que o valor toral de vendas diárias desse vendedor, poderá ser de $0, $50000 ou $100000. Logo, teremos que calcular P(Y = 0), P(Y = 50000) e P(Y = 100000).
Passo 2
Para montar a função de probabilidade de uma v.a. discreta, a gente precisa montar aquela tabelinha, com os possíveis valores de Y e a probabilidade de cada um desses valores acontecer.
Os possíveis valores a gente já tem: {0, 50000, 100000}, agora falta calcular a probabilidade de cada um.
Vamos começar por .
Para calcularmos o valor de P(Y = 0) devemos mapear cada aresta do diagrama, partindo do vértice de origem até o vértice de destino, o qual contém o valor da venda diária, nesse caso queremos chegar nos destinos que resultam em um valor de venda diária igual a 0.
Caminhando pelo diagrama, só temos dois caminhos que chegam em 0, e destaquei eles abaixo:
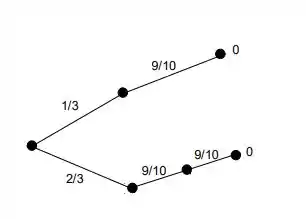
A partir desses dois ramos, podemos escrever que a probabilidade de vale:
Reparem que a gente seguiu multiplicando os valores que apareciam nos ramos e somamos essas multiplicações em seguida.
Passo 3
Podemos seguir o mesmo raciocínio para calcular P(Y = 50000) e P(Y = 100000), basta seguirmos seus respectivos ramos:
Passo 4
Agora que temos as probabilidades, podemos montar a tabelinha da distribuição da v.a. Y.

Passo 5
O valor total esperado será
Resposta
