Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 26
De uma caixa que contém três bolas pretas e três verdes, três bolas são selecionadas sucessivamente, cada uma sendo reposta na caixa antes que a próxima retirada seja feita. Determine a distribuição de probabilidade para o número de bolas verdes selecionadas.
Passo 1
Falaa, meu querido/minha querida. Vamos usar para representar o número de bolas verdes que são selecionadas em 3 tentativas, pode assumir os valores , , e .
Por causa da reposição das bolas, antes de cada retirada são 2 bolas verdes e 4 bolas pretas.
O que significa que a probabilidade de ser retirada uma bola verde a cada retirada é: .
E a probabilidade de retirar uma bola preta é: .
Portanto, nós temos a seguinte fórmula da distribuição de probabilidade:
Então, bora para os cálculos!!
Passo 2
Calculando a probabilidade de tirar nenhuma bola verde:
A probabilidade de tirar uma bola verde:
A probabilidade de tirar duas bolas verdes:
Por fim, a probabilidade de tirar as 3 bolas verdes:
Sendo assim, a distribuição de probabilidade para o número de bolas verdes selecionadas é:
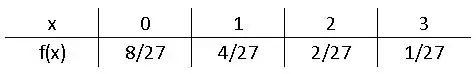
Resposta
Resolução nos passos anteriores.