Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Distribuição Normal

Produzido por Matheus dos Santos Soares
Ver Todos os Exercícios

Teoria

A distribuição normal, também conhecida como distribuição gaussiana é um modelo muito utilizado em probabilidade e estatística e serve para descrever de forma geral a frequência com que valores ocorrem num histograma.

-Hãm?! 😖

Calma, eu sei que esse conceito parece muito abstrato! Mas confia em mim, quando você entender, você vai pensar: “ahhh, isso faz TODO sentido!”. Pra isso, se liga nesse videozinho super completo que a gente preparou especialmente pra você 👇

📢 Clique para saber mais:

Distribuição Normal na Prática

Pra a gente entender bem o significado da distribuição normal, vamos analisar o peso de uma amostra de bebês recém-nascidos, com intervalos de .

É importante a gente ter em mente que peso é uma variável aleatória contínua, isso é, uma variável que pode assumir qualquer valor dentro de um intervalo. Por exemplo, podemos considerar o intervalo de peso entre e e a nossa variável vai poder assumir qualquer valor dentro desse intervalo!

A distribuição normal só vai funcionar quando estivermos falando de distribuições contínuas, beleza?!

Então mãos à obra! Vamos pegar todos os dados e construir um gráfico de frequência de peso desses recém-nascidos com intervalos de :

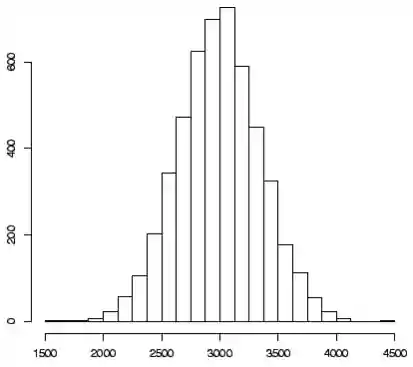
Histograma
Histograma

O nome desse gráfico é histograma e olhando pra ele, podemos dizer que, o peso “normal” do bebê recém-nascido é de , afinal a maioria dos bebês dessa amostra tem, em torno de . Por isso, se pegarmos um bebê aleatoriamente dentro dessa amostra, é muito mais provável que seu peso esteja mais próximo de do que de ou .

Tá começando a pegar a ideia de distribuição de probabilidade normal?!

Agora vamos prestar atenção no formato desse histograma. Se traçarmos uma curva sobre esse gráfico mostrando a tendência dos pesos dos recém-nascidos, obtemos mais ou menos isso:

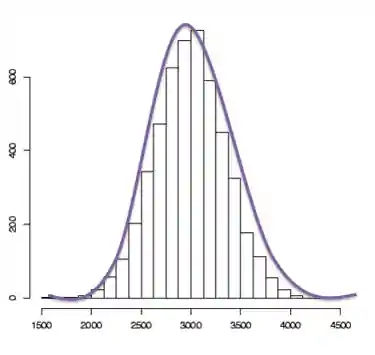
Sempre que os nossos dados tiverem esse formato de “sino”, dizemos que a variável aleatória contínua segue uma distribuição normal.

A ideia aqui é, a medida que aumentamos o número de bebês da amostra e diminuímos o intervalo entre os pesos, mas claro vai ficar esse formato de “sino”.

Então, se a gente pegarmos todos os bebês recém-nascidos do mundo e tender o intervalo de peso a zero, vamos ter a seguinte curva:

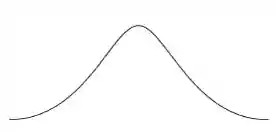
Curva de distribuição normal.
Curva de distribuição normal.

É claro que na prática é um pouquinho impossível analisar todos os bebês do mundo e a nossa intenção nem é essa! 🤣

Lá com os bebês a gente já conseguiu perceber que o peso dos bebês segue uma distribuição gaussiana, então a gente pode dizer, sem medo de ser feliz, que na média um bebê recém-nascido pesa !

Parâmetros da Distribuição Normal

Agora, vamos falar das características que são o coração da distribuição normal. Note que quando olhamos para esse formato específico do gráfico percebemos que ele é simétrico em relação ao seu centro:

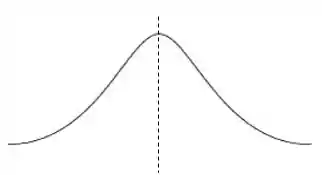
Simetria da Curva Gaussiana
Simetria da Curva Gaussiana

Esse valor central é representado pela letra grega e é o que chamamos de média da população.

Além disso, note que os demais valores se afastam da média. Para medir essa dispersão em torno da média usamos um parâmetro chamado desvio padrão .

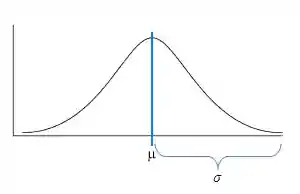
Média e desvio padrão.
Média e desvio padrão.

O inconveniente do desvio padrão é que ele pode assumir valores positivos ou negativos, então na prática vamos usar a variância, representado por , que nada mais é do que o desvio padrão elevado ao quadrado!

Esse dois são os parâmetros que temos e são o coração da distribuição normal, então guarda eles com carinho!

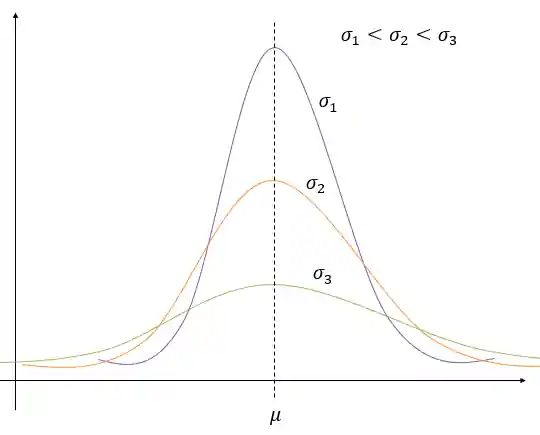
Note que quanto maior o meu , mais dispersos em torno da média estão os dados e mais achatado fica o gráfico:

Podemos escrever uma expressão matemática que descreve o gráfico da distribuição normal em função da média e da variância:

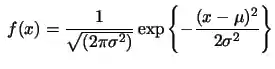
Função da curva Gaussiana.
Função da curva Gaussiana.

Ela é bem complexa, não é? Mas, não precisa se desesperar não porque na prática a gente nem vai usar ela!

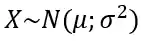
Para simplificar a nossa vida, quando uma variável aleatória contínua é descrita pela distribuição normal, nós usamos a seguinte notação:

Notação
Notação

Essa notação diz pra gente que a variável aleatória segue uma distribuição normal, com média e variância .

Por exemplo, quando escrevemos:

Queremos dizer que segue uma distribuição normal com média e variância .

Distribuição Normal Padrão

Para uma variável aleatória continua ser normal, ela precisa seguir aqueles critérios, obedecendo aqueles parâmetros, certo?

Mas pensando nisso, teremos infinitas curvas, percebe? Com média igual a Isso sem contar as diferenças de variâncias.

A parte boa aqui, é que a principal normal que você precisa saber é a normal padrão! Se uma variável aleatória tem distribuição Normal com média igual a 0 e variância igual a 1, dizemos que ela tem distribuição Normal Padrão.

A notação que usamos nesse caso é essa daqui:

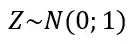
Normal padrão
Normal padrão

-Mas porque essa distribuição normal padrão é tão importante?

Porque essa normal padrão possuiu uma tabela com todos os valores de função de distribuição acumulada que vamos precisar. Em outras palavras, se eu quero calcular a probabilidade de ser menor ou igual a um valor , basta eu olhar nessa tabela que eu vou encontrar:

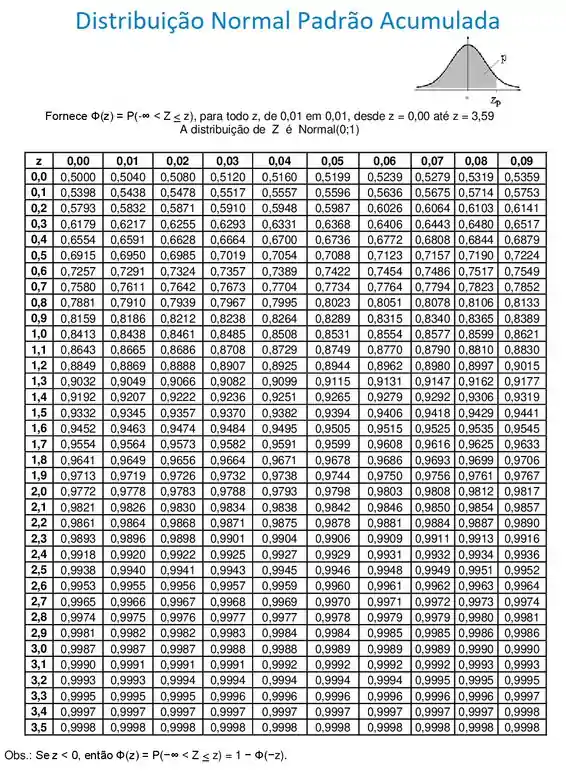
Tabela de distribuição normal.
Tabela de distribuição normal.

Padronização

-Então, pra calcular probabilidades de uma variável aleatória que segue uma normal padrão eu olho na tabela, mas e se a normal não for padrão? Eu tenho que usar aquela fórmula toda complicada que descreve o gráfico?

NÃOOOOO! O que vamos fazer é utilizar um procedimento simples de padronização, de modo que uma normal que não seja padrão passe a ser padrão e aí nós conseguimos olhar a probabilidade na tabela.

É simples o processo de transformação de uma variável aleatória que segue uma distribuição normal não padrão, , em uma varável aleatória que segue uma distribuição normal padrão, .

Vamos supor que temos:

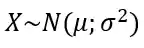
Distribuição normal
Distribuição normal

Para transforma-la em uma variável , definiremos dessa maneira aqui:

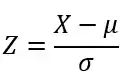
Variável z
Variável z

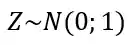
E esse segue a normal padrão:

Normal padrão.
Normal padrão.

Assim, se queremos calcular probabilidade de ser menor ou igual a um valor , faremos:

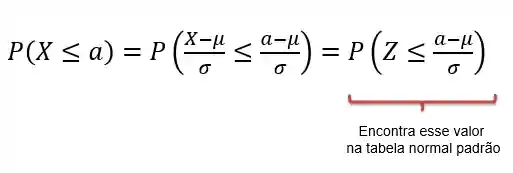
Cálculo de probabilidade.
Cálculo de probabilidade.

Exemplo: Cálculo de Probabilidade

Vamos supor que uma variável aleatória segue uma distribuição normal com média igual a e variância igual a . Quanto seria ?

Beleza, então vamos ver o que temos:

E queremos:

Usaremos:

Assim:

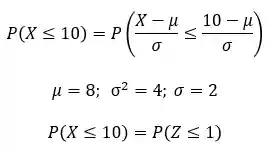
Cálculo de probabilidade: Resposta
Cálculo de probabilidade: Resposta

Agora, basta procurar na tabela o valor de .

Sacou? Super legal, não é?

Agora que você tá sacando tudo sobre distribuição normal, bora praticar com exercícios?!

Parâmetros da Distribuição Normal

Distribuição Normal Padrão

Padronização

Exercícios Resolvidos

Exercício Resolvido #1

UERJ-lista 2 prof Fabiano-14

Suponha que o tempo necessário para atendimento de clientes em uma central de atendimento telefônico siga uma distribuição normal de média de 8 minutos e desvio padrão de 2 minutos.

a) Qual é a probabilidade de que um atendimento dure menos de 5 minutos?

b) E mais do que 9,5 minutos?

c) E entre 7 e 10 minutos?

d) 75% das chamadas telefônicas requerem pelo menos quanto tempo de atendimento?

Passo 1

(a)

Se a gente chamar de X a v.a. que representa o tempo necessário para atendimento de clientes em uma central de atendimento telefônico.

De acordo com o enunciado,

X   ~   N o r m a l ( 8 ; 4 )

Já que a média é: μ = 8 .

E o desvio padrão é:   σ = 2 .

Passo 2

Probabilidade de durar menos 5 minutos é:

P X < 5 =   ?

Fazendo a padronização:

P X < 5 = P Z < 5 - 8 2

= P Z < - 1,5

Invertendo os sinais:

= P ( Z > 1,5 )

= 1 - P ( Z < 1,5 )

= 1 - Φ 1,5

Usando a tabela da Normal, cruzando a linha 1,5 com a coluna 0,00, encontramos que:

Φ 1,5 = 0,9332

Logo:

P X < 5 = 1 - 0,9332 = 0,0668

Passo 3

(b)

P X > 9,5 =   ?

Padronizando..

= P Z > 9,5 - 8 2

= P Z > 0,75

= 1 - P Z < 0,75

= 1 - Φ 0,75

Usando a tabela novamente..

Φ 0,75 = 0,7734

P X > 9,5 = 1 - 0,7734

P X > 9,5 = 0,2266

Passo 4

(c)

P 7 < X < 10 =   ?  

Padronizando...

= P 7 - 8 2 < Z < 10 - 8 2

= P - 0,5 < Z < 1

= Φ 1 - Φ - 0,5

Usando a tabela..

Φ 1 = 0,8413

Com Φ ( 0,5 ) e Φ ( - 0,5 ) temos que:

Φ - 0,5 = 1 - Φ 0,5 = 1 - 0,6915

= 0,3085

Pra fechar então:

P 7 < X < 10 = 0,8413 - 0,3085

P 7 < X < 10 = 0,5328

Passo 5

(d)

Beleza, agora pensa aqui comigo!

Nós queremos saber, ao menos quanto tempo é necessário para atender 75% das chamadas...

Então, sobre esse tempo, digamos que ele seja um valor k, 75% das chamadas demoram MENOS que esse valor. Com isso, podemos escrever que a probabilidade do tempo da chamada ser menor que k é igual a 75%, certo?

P X < k = 0,75

Padronizando..

P Z < k - 8 2 = 0,75

Φ k - 8 2 = 0,75

Ou seja:

Φ k - 8 2 = 0 , 7 5

O valor da tabela que nos dá 0,75 de probabilidade é o 0,67 .

Com isso:

k - 8 2 = 0,67

k - 8 = 1,34

k = 9,34   m i n u t o s

k ≅ 9,3   m i n u t o s

Resposta

a   0,0668

b   0,2266

c   0,5328

d   9,3   m i n u t o s

Exercício Resolvido #2

UFRJ-P1-2013.2-3

Suponha que a altura dos homens em uma certa cidade tem distribuição Normal com média μ = 1,80 m e desvio padrão, σ = 10 c m . Calcule:

  1. A probabilidade de um homem ter mais de 1,90 m   de altura.
  2. O valor em metros abaixo do qual estão as alturas de 30% desses homens.

Passo 1

O exercício diz pra gente o que ? Que temos uma v.a. X ;

X : a l t u r a   d e   h o m e n s   d e   u m a   c i d a d e

E que essa v.a. segue uma distribuição Normal, com μ = 1,80 m e σ = 10 c m .

Lembrando que os parâmetros da Normal são μ e σ ² .

X   ~   N o r m a l   1,80 ; 10 2

Maaaas.. atenção, vamos ajeitar as unidades. Um valor tá em metros e o outro em centímetros, vou colocar tudo em centímetros.

X   ~   N o r m a l   ( 180 ; 10 2 )

Beleza?!

Passo 2

(a)

O exercício quer que a gente calcule a probabilidade de um homem ter mais de 1,90 m   de altura, ou seja, P ( X > 190 ) , concorda ?

Aprendemos que o processo de padronização utiliza a seguinte carinha:

Z = X -   μ σ

Assim, fazendo o processo de padronização da Normal:

P X > 190 = P Z > 190 - 180 10

        = P Z > 1 , 00

Que é a mesma coisa que

                        = 1 - P Z < 1 , 00

        = 1 - Φ 1 , 00

Procurando na tabela o valor de Φ ( 1 ) , cruzando a linha 1 com a coluna 0,00, vamos ter

Φ 1 = 0,8413

Portanto,

P X > 190 = 1 - 0,8413

= 0,1587

Ou seja, a probabilidade de um homem ter mais de 1,90 m   de altura é de 15%.

Passo 3

(b)

A gente quer o valor em metros abaixo do qual estão 30% dos homens dessa cidade. Vamos chamar esse valor de k .

A gente sabe então que:

P X < k = 0,30

Usando o processo de padronização:

P Z < k - 180 10 = 0,30

Tá! Mas qual valor de Z que na tabela eu encontro probabilidade 0,30? Nenhum, porque na tabela só tem valores de probabilidade maiores que 0,5, lembra?

Só que como a Normal tem simetria, procurar um valor z que tenha probabilidade 0,30 é o mesmo que procurar um valor que tenha probabilidade 1 - 0,3 → 0,7 e trocar o sinal.

Se você olhar aí na sua tabela, o valor que dá a prob. mais próxima de 0,70 é o z = 0,52 .

Então a gente vai usar na verdade o z = - 0,52 .

Passo 4

Como:

z = k - 180 10

E z = - 0,52 , então:

- 0,52 = k - 180 10

k = 180 - 5,2

k = 174,8   c m

Como o problema pede em metros, nossa resposta final é:

k = 1,748   m

Resposta

a   0,1587

b   1,748   m

Exercício Resolvido #3

PUCRIO-P2-2013.2-3

A vazão instantânea de um rio ( m 3 / s ) em um determinado momento do mês de março (mais úmido) pode ser modelada por uma v.a. normal com média e variância iguais a 100 . Por motivos de auditoria, exige-se uma memória de cálculo para todos os passos do projeto (explicação formal dos cálculos realizados). Assim, responda as seguintes questões:

  1. Desejamos dimensionar a potência de uma hidrelétrica a ser construída na cabeceira deste rio. Para isso, precisamos encontrar o valor crítico de vazão instantânea do mês mais úmido que não é excedido com 95 % de probabilidade. Calcules este valor.
  2. Calcule a probabilidade de um dado momento do mês de março apresentar valores entre 88 e 110 m ³ / s .
  3. Suponha que tenhamos uma amostra de 6 medições de vazões instantâneas dos meses de março. Calcule a probabilidade da média destas vazões ser superior a 110 m ³ / s .

Dado: Distribuição normal de uma média x - : N o r m a l     μ   ; σ 2 n

Passo 1

(a)

X → vazões instantâneas do mês de março.

De acordo com o enunciado, a gente tem que:

X   ~   N o r m a l   100 ; 100

Primeiro o exercício quer que a gente calcule pra qual valor de X , temos 95 % das vazões abaixo.

Reescrevendo isso...

P X ≤ a = 95 %

Temos que calcular esse a aí, que é o valor de X que não é ultrapassado por 95 % dos valores possíveis.

Passo 2

Primeiro a gente padroniza, como sempre nas questões de Normal.

P X ≤ a = P Z ≤ a - 100 10 = 0,95

Agora vamos na tabela da Normal procurar pelo valor que nos dá 0,95 como probabilidade. Pra isso, vamos caçar o 0,95 dentro da tabela e ver o valor que gera ele.

z = 1,64

Passo 3

Agora é só igualar...

a - 100 10 = 1,64

a = 116,4   m ³ / s

Você poderia usar 1,645 também, já que o 0,95   está entre 0,9495 e 0,9505 que são os valores tabelados. Com isso:

a = 116,45   m ³ / s

Passo 4

(b)

Vamos calcular...

P 88 < X < 110 =   ?

Padronizando...

P 88 - 100 10 < Z < 110 - 100 10 = P - 1,2 < Z < 1

= P Z < 1 - P Z < - 1,2

Trocando o sinal de menos de dentro dali...

= P Z < 1 - P Z > 1,2

= P Z < 1 - 1 - P Z < 1,2

Olhando na tabela...

= 0,8413 - 1 + 0,8849

= 0,7262

Passo 5

(c)

Humm, agora vamos tratar de uma distribuição pra média x ¯ .

Como a gente viu, uma média tem distribuição Normal assim...

N o r m a l     μ   ; σ 2 n

Então nesse caso teremos:

X ¯   ~   N o r m a l   100   ; 100 6

Passo 6

Vamos calcular o que foi pedido agora...

P X ¯ ≥ 110 =   ?

Mesmo processo.. padronizamos...

P X ¯ > 110 = P Z > 110 - 100 10 6

= P Z > 2,45

= 1 - P Z < 2,45

Olhando na tabela..

= 1 - 0,9929

= 0,0071

Resposta

a   116,45   m ³ / s

b   72,62 %

c   0,71 %

Exercício Resolvido #4

UFF-VR-3

A espessura de uma forja de duralumínio (em mm) é normalmente distribuída com μ = 22,86 e σ = 0,0762 . Os limites de especificação foram dados como 22,86 ± 0,127   m m .

  1. Que percentual de forjas será defeituoso?
  2. Qual é o valor máximo permissível para σ que permitirá que não exista mais de 1 forja defeituosa em 100 se as espessuras forem de μ = 22,86 e σ ?

Passo 1

X → v.a. que simboliza a espessura de uma forja de duralumínio.

X   ~   N o r m a l   22,86   ; 0,0762 2

Os limites da especificação são 22,86 ± 0,127

= 22,733   ; 22,987

Temos que calcular o percentual de forjas que será defeituoso, ou seja, que estarão fora dos limites de especificação.

Poderíamos calcular o percentual acima de 22,987 e somar com os abaixo de 22,733 . Mas acho mais prático calcular o percentual que estará dentro dos limites e tirar de 100 % .

Passo 2

Calculando os que estão dentro do limite, sem defeito.

P 22,733 < X < 22,987 =   ?

Padronizando...

P 22,733 - 22,86 0,0762 < Z < 22,987 - 22,86 0,0762

P - 1,67 < Z < 1,67

= P Z < 1,67 - P Z < - 1,67

Tirando o sinal de negativo...

= P Z < 1,67 - P Z > 1,67

Mudando o sinal de maior por um de menor...

= P Z < 1,67 - 1 - P Z < 1,67

= 2 . P Z < 1,67 - 1

Olhando na tabela da Normal...

= 2 × 0,9525 - 1

= 0,905

Passo 3

Com isso, o valor que queremos, que representa o percentual de defeituosos será:

1 - 0,905 = 0,095

Que é o mesmo que 9,5 % .

Passo 4

Letra B: O que queremos nesse exercício que o valor da probabilidade de não ser defeituoso abaixo seja igual a 99% (1 defeituosa em 100). E por que igual e não menor ou igual? Pois ele quer o maior valor possível e isto ocorre no 1%

P 22,733 < X < 22,987 =   0,99

Passo 5

Padronizando...

P 22,733 - 22,86 σ < Z < 22,987 - 22,86 σ = 0,99

P - 0,127 σ < Z < 0,127 σ = 0,99

P Z < 0,127 σ - P Z < - 0,127 σ = 0,99

Tirando o sinal de negativo...

P Z < 0,127 σ - P Z > 0,127 σ = 0,99

Mudando o sinal de maior por um de menor...

P Z < 0,127 σ - 1 - P Z < 0,127 σ = 0,99

2 . P Z < 0,127 σ - 1 = 0,99

P Z < 0,127 σ = 1 + 0,99 2 = 0,995

Olhando na tabela da Normal...

0,127 σ = 2 , 58

0,127 2,58 = σ

σ = 0,04 92

Resposta

a ) 9,5 %

b ) σ = 0,0488

Exercício Resolvido #5

UFF-2°VE-1

A dureza Rockwell de uma liga particular é distribuída normalmente, com uma média de 70 e um desvio padrão de 4 .

  1. Determinar a probabilidade da dureza estar entre 62 e 72 .
  2. Se o intervalo aceitável para a dureza fosse ( 70 - c ,   70 + c ) , para qual valor de c teríamos 95 % de todos os espécimes com dureza aceitável?

Passo 1

a)

Chamando de X → valor da dureza Rockwell.

A gente tem que:

X   ~   N o r m a l   70,16

Já que a média é μ = 70 , e o desvio padrão é σ = 4 .

Temos que calcular:

P 62 < X < 72 =   ?

Passo 2

Pra isso, primeiro padronizamos...

P 62 < X < 72 = P 62 - 70 4 < Z < 72 - 70 4

= P - 2 < Z < 0,5

Isso é a mesma coisa que:

P Z < 0,5 - P Z < - 2

Primeiro vamos mudar esse negativo aí...

P Z < - 2 = P Z > 2

Concorda? A gente faz essa adaptação pra poder procurar o valor na tabela, já que lá não tem valores negativos.

Pra fechar:

P Z > 2 = 1 - P Z < 2

Aí:

P Z < 0,5 - P Z < - 2

= P Z < 0,5 - 1 - P Z < 2

= P Z < 0,5 + P Z < 2 - 1

Procurando esses valores na tabela da Normal...

= 0,6915 + 0,9773 - 1

= 0,6688

Passo 3

b)

O que o exercício pede é qual o valor de c pra que a afirmação abaixo seja verdade.

P 70 - c < X < 70 + c = 0,95

Vamos padronizar...

P 70 - c - 70 4 < Z < 70 + c - 70 4 = 0,95

P - c 4 < Z < c 4 = 0,95

P Z < c 4 - P Z < - c 4 = 0,95

P Z < c 4 - 1 - P Z < c 4 = 0,95

2 . P Z < c 4 - 1 = 0,95

P Z < c 4 = 0,975

Entendeu o que eu fiz? Padronizei e depois fui resolvendo igual a gente fez na letra (a). Só que no final agora a gente tem que descobrir primeiro qual o valor da tabela que nos dá probabilidade 0,975 .

Passo 4

Vamos caçar dentro da tabela o 0,975 ou o mais perto e aí a gente vê o valor do z , cruzando linha e coluna...

Fazendo isso...

z = 1,96

c 4 = 1,96

c = 7,84

Resposta

a   0,6688

b   c = 7,84

Exercícios de Livros Relacionados

Uma corrente elétrica oscilante pode ser considerada como uma variável aleatória uniformemente distribuída sobre o intervalo (9,11). Se essa corrente passar em um resistor de 2 ohms, qual será a fdp d
A resistência à compressão de amostras de cimento pode ser modelada por uma distribuição normal, com uma média de 6000 quilogramas por centímetro quadrado e um desvio-padrão de 100 quilogramas por cen
Um combustível para foguetes deve conter uma certa percentagem X de um componente especial. As especificações exigem que X esteja entre 30 e 35 por cento. O fabricante obterá um lucro líquido T sobre
Sabe-se que os erros, em certo dispositivo para medir comprimentos, são normalmente distribuídos com valor esperado zero e desvio-padrão 1 unidade. Qual é a probabilidade de que o erro na medida seja
Use a Tabela III do Apêndice para determinar as seguintes probabilidades para a variável aleatória normal padrão Z : P ( - 1Z1 ) P ( - 2Z2 ) P ( - 3Z3 ) P ( Z3 ) P ( 0Z1 )