Distribuição Exponencial
Produzido por Jorge Alberto NascimentoTeoria
Fala aí! Seja bem vindo ao Responde Aí! Bora aprender tudo sobre Distribuição Exponencial?!
O que é uma Distribuição Exponencial?
A distribuição exponencial é comumente usada para modelar probabilidades que vão decaindo com o tempo de forma exponencial! Pra ficar mais claro como ela funciona vamos imaginar o seguinte exemplo:
Você comprou um celular e gastou um bom dinheiro nele! Mas sabe como é a vida né, eventualmente ele vai parar de funcionar. Então, você quer saber qual a probabilidade do aparelho continuar funcionando depois de 3 anos de uso, sabendo que em média, esse aparelho dura 2 anos. Concorda comigo que a medida que o tempo passa, a probabilidade do celular continuar funcionando diminui?!
Pra resolver esse problema vamos usar a distribuição exponencial! Vamos lá?
📢 Clique para ver mais:
Como Calcular a Distribuição Exponencial
Como falamos lá em cima, a gente usa a distribuição exponencial pra modelar probabilidades que vão diminuindo com o tempo, assim como a probabilidade do seu celular continuar funcionando!
Podemos modelar essa função de densidade da seguinte forma:
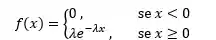
Show! Mas o que isso significa!? Pra saber isso e muito mais, confere esse vídeo super completo que o Responde Aí preparou pra você! 🧡
Voltando à nossa função densidade, nela temos. No caso do nosso exemplo:
E dizemos que essa variável é dada por:
Onde:
Lembrando que, sempre que falamos de esperança, estamos falando da média. No caso do nosso celular, a esperança era de que ele durasse só 2 anos, logo:
Com isso, temos a função de densidade para o celular:
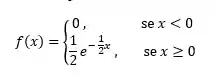
O gráfico dessa função tem essa carinha aqui:
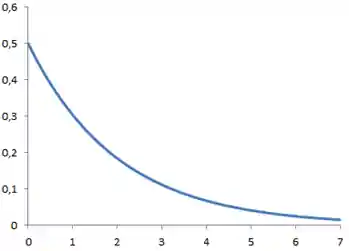
E no nosso exemplo, queremos a probabilidade de que o aparelho dure mais que 3 anos. Se você reparar, podemos abordar esse problema de uma forma mais fácil:
Repare que dessa forma estamos “tirando” toda a possibilidade do celular durar menos de 3 anos, sacou? Para resolver isso podemos usar a famosa Função de Distribuição Acumulada!
Função de Distribuição Acumulada
A Função de Distribuição Acumulada nos dá os valores somados de todas as probabilidades até um certo ponto, que é simbolizado por
Então, se a gente fizer as integrais necessárias pra achar a FDA, vamos ter essa carinha aqui:
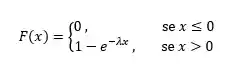
Maas pera, se você reparar, nosso exemplo já temos o valor de
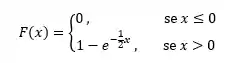
Onde o gráfico dessa função teria essa carinha:
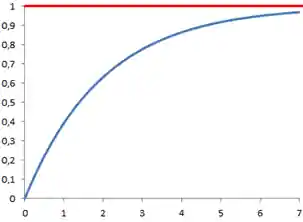
Dessa forma, como queremos calcular a probabilidade do celular durar mais de
Onde
Perda de Memória da Exponencial
Sabendo que
O que temos nesse caso acima é uma probabilidade condicional. Em outras palavras:
Repara que a interseção de
Se a gente pegar a fórmula da probabilidade acumulada da exponencial:
Que podemos escrever como:
Onde:
Logo:
Então a probabilidade do meu aparelho velho funcionar pelo menos 3 anos sabendo que ele já funcionou por 2 é a mesma de eu comprar um aparelho novinho e ele funcionar por pelo menos 1 ano! Essa é a perda de memória da distribuição exponencial!
De uma forma geral, podemos dizer que:
Distribuição Exponencial e Distribuição de Poison
Existe uma relação entre a distribuição exponencial e a de Poisson. Vamos ver um exemplo?!
Suponha que ocorrem em média 2 assassinatos numa cidade por dia. Se M representa o número de assassinatos por dia e segue o modelo de Poisson, e T representa o intervalo de tempo, em dias, entre assassinatos sucessivos. Forneça a expressão matemática da função de densidade de T.
A relação entre a distribuição exponencial e a de Poisson vai funcionar da seguinte forma:
Em outras palavras, se
Lembrando que a primeira fórmula é a FDA da exponencial, e a segunda é a função de probabilidade da Poisson. A diferença aqui é que
Por isso, temos a nossa função de densidade:
Agora vamos praticar com exercícios?!
Função de Distribuição Acumulada
Perda de Memória da Exponencial
Distribuição Exponencial e Distribuição de Poison
Exercícios Resolvidos
Exercício Resolvido #1
PUCRIO-P2-2013.1-1c)
Como você definiria uma aplicação para uma v.a. que segue um modelo exponencial? Dê um exemplo real onde você recomendaria a utilização deste modelo.
Passo 1
Bom, uma distribuição exponencial é uma distribuição contínua que serve para analisar tempos de duração de um determinado experimento.
Um exemplo de aplicação real seria o tempo entre chamadas em um CallCenter.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
CEFET-LISTA VA- REGINA-10
O tempo entre a chegada de mensagens eletrônicas em seu computador é distribuído exponencialmente, com uma média de duas horas.
- Qual é a probabilidade de você não receber uma mensagem durante o período de duas horas?
- Se você não tiver recebido uma mensagem nas primeiras quatro horas, qual será a probabilidade de você não receber uma mensagem nas próximas 2 horas?
Passo 1
(a)
Se é a v.a. que representa o tempo entre a chegada de mensagens eletrônicas.
Ele diz que a média é de 2 horas, e a gente sabe que a expressão para a média de uma distribuição exponencial é:
Então:
Passo 2
Agora queremos calcular a probabilidade de não haver ligações num período de 2 horas:
Temos que usar a relação da exponencial com Poisson:
Passo 3
Agora só substituir, com .
Passo 4
A probabilidade de não receber ligações em um intervalo de 2 horas continua sendo o mesmo, independente do que aconteceu antes:
Resposta
Exercício Resolvido #3
UFRJ-P1-2014.2.-3B
Por saber que há uma grade procura por imóveis em determinada região muito valorizada, uma construtora decide comprar um terreno e construir uma casa nesse local.
b) O prazo necessário para realizar a obra pode ser encarado como uma variável aleatória com distribuição Exponencial. Com base na sua experiência, a construtora presume que uma obra como essa levaria em média meses para ficar pronta. Que prazo para entrega das chaves, a partir do início da obra, deve ser informado aos possíveis interessados na compra da casa? Admita que a construtora deseja ser capaz de cumprir esse prazo com de probabilidade.
Passo 1
(b)
O tempo pra realização da obra segue uma distribuição Exponencial com média meses.
A gente sabe que uma distribuição Exponencial tem média, ou esperança:
Onde tempo pra conclusão da obra.
E o texto diz que essa média é de meses.
Precisamos ver qual o tempo que deve ser informado pra conclusão da obra, pra que a construtora cumpra dos casos.
Passo 2
Vamos precisar da função acumulada da Exponencial, que é:
Substituindo
Queremos o que nos dá .
Passo 3
Resolvendo essa equação aí:
Aplica dos dois lados:
Arredondei pra cima.
Resposta
Exercício Resolvido #4
UFRJ-P1-2014.1-3a
Ocorrem, em média, 10 desintegrações por minuto numa amostra de material radioativo. Suponhamos que o número, , de desintegrações por minuto seja uma variável aleatória de Poisson e que seja o intervalo de tempo em minutos entre duas desintegrações sucessivas.
- Forneça a expressão matemática da função de densidade de ;
Obs.: Lembre-se de que existe uma relação entre os modelos de Poisson e Exponencial.
Passo 1
Temos:
Se a gente sabe que acontecem, em média, 10 desintegrações por minuto, e esperança de é s.
Por outro lado,
Então, :
A gente aprendeu a relação entre Poisson e Exponencial, que se encaixa perfeitamente nesse caso, então:
Desse jeito, a função de densidade de vai ser: