Teorema Central do Limite
Teoria
Fala aí, seja bem vindo ao Responde Aí! Bora aprender sobre Teorema Central do Limite?
O que diz o Teorema Central do Limite?
O Teorema Central do Limite (TCL), também chamado de Teorema do Limite Central, diz que a soma de N variáveis independentes (x) com mesma distribuição, se aproxima de uma distribuição normal a medida que N aumenta.
-Hãam? 😖
Pra você entender melhor, eu separei um videozinho super completo, com exemplos, exercícios de prova e muito mais! 👇
📢 Clique para ver mais:
Teorema do Limite Central: Exemplo
Seja a variável aleatória:
Que pode assumir os valores
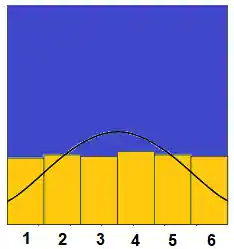
Repara que não chegamos a nada parecido com uma distribuição normal! Isso porque no teorema central do limite é a a distribuição da média amostral que se aproxima da normal. Ali, nós estamos olhando para a distribuição da variável em si. Agora vamos refazer nosso experimento!
Imagina então que agora eu tenho 2 dados, e vou lança-los 100 vezes de novo. Em cada lançamento, eu quero a média do valor dos 2 dados. Plotando o gráfico da distribuição dessa média amostral, teremos:
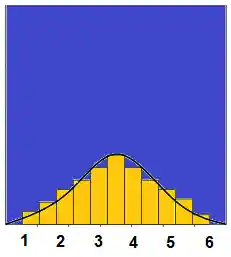
Nesse caso, dizemos que a amostra contém 2 valores (n=2), pois foram lançados 2 dados. O TCL só pode ser aplicado quando n≥30, que é quando a amostra é suficientemente grande. Para o caso do dado, o gráfico para a média amostral do lançamento de 30 dados seria:
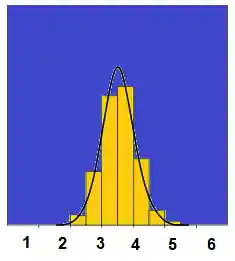
Ainda mais próximo da normal! Quanto maior o n da sua amostra, mais próximo a distribuição da média amostral será da normal. O teorema do limite central diz que:
Ou seja, a média amostral segue uma normal com média igual a média populacional e desvio padrão dado por
Agora vamos praticar com exercícios?!
Teorema do Limite Central: Exemplo
Exercícios Resolvidos
Exercício Resolvido #1
PUCRIO-P2-2013.2-
b) Seja uma sequência de v.a.’s independentes com distribuição . Se , quem é a distribuição de ? E da v.a. .
Passo 1
Temos que é uma amostra aleatória de uma v.a. , com isso todas as ’s tem a mesma distribuição , beleza?
Se eu chamar , pelo Teorema Central do Limite a gente diz que tem distribuição.
Com:
Passo 2
Agora se eu fizer , é a mesma ideia, só dividir os valores que a gente viu por .
Com:
Resposta
Exercício Resolvido #2
UFRJ-P1-2013.1-4
e representam os valores (em reais) que as ações A1 e A2, respectivamente, terão daqui a um ano. Como sabemos, o comportamento caótico da bolsa de valores implica que e podem ser considerados aleatórios. Suponha, mais especificamente, que:
- é modelada por uma distribuição Normal com média de 30 reais e variância de 100 reais²;
- é modelada por uma distribuição Normal com média de 60 reais e variância de 400 reais²; e
- as cotações dessas duas ações são independentes.
Um investidor comprou hoje 300 ações A1 a 25 reais cada uma, e 200 ações A2 a 40 reais cada uma.
- Quais são a distribuição, a esperança e o desvio padrão do valor total que a carteira de ações deste investidor terá dentro de um ano?
- Qual é a probabilidade de que essa a carteira de ações tenha se valorizado em pelo menos 50% depois de um ano?
Passo 1
(a)
Vamos chamar de:
De acordo com o enunciado:
Passo 2
Calcular .
Sabendo que e :
Passo 3
Calcular
Sabendo que e .
Com isso.
Como é a soma de duas variáveis de distribuição Normal, então:
Passo 4
(b)
Primeiro a gente tem que saber quanto custou o portifólio no momento da compra. De acordo com o enunciado, o valor total foi:
Pra acontecer valorização de pelo menos 50%. O portifólio tem que estar valendo depois de um ano o valor de:
Passo 5
Pra saber a probabilidade disso acontecer, a gente precisa calcular:
Pradronizando...
Se procurar na tabela, você vai ver que .
Então:
Resposta
Exercício Resolvido #3
UFRJ-P1-2014.1-4
Um pequeno restaurante tem uma receita diária - da qual já foi descontado o gasto com ingredientes - cuja média é de 800 reais e cujo desvio padrão é de 300 reais. A despesa mensal do restaurante com mão de obra, encargos, manutenção, etc., é da ordem de 12.000 reais.
- Se ele funciona na base de 25 dias por mês, qual a probabilidade de que esse negócio dê um lucro de pelo menos 7.000 reais por mês?
- Digamos que, em um determinado mês, o restaurante só vai ficar aberto durante 20 dias. Mas, ainda assim, deseja-se manter a meta de um lucro mínimo de 7.000 reais. Para quanto deveria aumentar a média da receita diária para que nesse mês, uma vez mantido o desvio padrão da receita diária em 300 reais, essa meta fosse atingida com probabilidade 95%?
Obs.: Admita que em ambos os casos o tamanho amostral é suficientemente grande para que seja válida a aproximação fornecida pelo Teorema Central do Limite.
Passo 1
(a)
Vamos chamar de:
A gente quer calcular
De acordo com o enunciado.
Já que são 25 dias de funcionamento e que as despesas fixas somam 12.000.
Passo 2
Se a gente quer é o mesmo que querer.
Só que de acordo com o teorema central do limite, quando a gente tem um somatório de um número grande de v.a. com mesma distribuição podemos aproximar por uma Normal.
Com isso.
Onde:
Passo 3
Concluindo, fazendo o processo de padronização da Normal.
Procurando na tabela.
Passo 4
(b)
Vamos ter dias e agora (valor desconhecido)
A situação é bem parecida com a anterior, tirando a mudança de . A diferença é que agora o exercício deu o valor da prob. final e quer o valor de referente.
Sendo que.
Pelo teorema central do limite aproximaremos.
Passo 5
Concluindo, fazendo o processo de padronização da Normal.
O valor da tabela que nos dá prob. de 0,95 é 1,64. Porém como estamos trabalhando com não podemos esquecer de multiplicar por
Então, com isso.
Resposta
Exercício Resolvido #4
Lista de Exercício Probest – Cap 6, IM – UFRJ.
Uma instituição de caridade deseja realizar uma obra que custa em sua sede. Entre os contribuintes habituais dessa instituição, cada um pode contribuir com algo em torno de um desvio padrão de . Se 30 dessas pessoas se quotizarem para levantar fundos com essa finalidade, qual a probabilidade de que eles consigam o montante necessário?
Passo 1
Vamos chamar a quantia que cada contribuinte pode doar de . Sabemos que:
Mas nós estamos tratando de 30 pessoas, então vamos ter 30 quantias doadas: ().
E os fundos levantados vão ser a soma de as 30 quantias doadas, certo? Vamos criar outra v.a. para representar a soma de todas essas doações, ou seja, a soma dos :
Para o montante necessário ser atingido, precisamos que todas as doações somadas resultem em pelo menos o custo da obra (), então:
E é a probabilidade disso acontecer que temos que calcular, ou seja: .
Mas qual a distribuição de ? Precisamos saber isso para calcular essa probabilidade. Como é uma soma de várias v.a’s ( já é grande o suficiente) independentes que seguem a mesma distribuição, podemos dizer que vai ser aproximadamente uma distribuição Normal:
Substituindo os valores:
Passo 2
Então agora podemos calcular . Padronizando (já que segue uma Normal):
Para tirar o negativo daí, invertemos o sinal de :
Procurando esse cara na tabela da Normal temos que...
Então:
Resposta
Exercício Resolvido #5
Lista de Exercício Probest – Cap 6, IM – UFRJ.
Uma companhia de seguros emitiu apólices para 10000 pessoas, todas da mesma faixa etária. A probabilidade de morte durante um ano é de 0,006 para cada pessoa nessa faixa etária. Em um dia pré-fixado, todos os segurados depositam 12 u.m. e, se algum deles morrer dentro de 1 ano, seus beneficiários receberão 1000 u.m. da seguradora. Qual a probabilidade de que em 1 ano:
(a) A companhia tenha prejuízo?
Passo 1
Vamos representar o lucro da seguradora no ano por pessoa por , e essa v.a. pode assumir dois valores:
E nós sabemos que a probabilidade de uma pessoa morrer é , então:
E de não morrer, vai ser a complementar de , ou seja, :
Lembrando da fórmula da esperança, podemos calcular :
E pela fórmula da variância, calculamos :
O lucro total vai ser dado pela soma dos lucros vindos de todas as pessoas:
Podemos aproximar a uma distribuição normal então, certo? Pelo Teorema Central do Limite! Já que são muuuitas v.a.’s com mesma distribuição e independentes somadas. Então:
Lembrando que e que já calculamos :
Passo 2
Agora podemos calcular o que foi pedido. A probabilidade da companhia ter prejuízo é a probabilidade do lucro total ser menor que zero:
Padronizando isso aí, já que segue uma Normal:
Invertendo o sinal para tirar o negativo:
Usando a probabilidade complementar para deixar o sinal como (no mesmo sentido que vamos procurar na tabela):
Cara, mas não tem esse valor na minha tabela, e agora??? Repara comigo que quando os valores vão crescendo, a gente se aproxima cada vez mais de uma probabilidade igual a , então vamos dizer que:
Entonnn...
Ou seja, a probabilidade da companhia ter prejuízo é praticamente zero!
Parece que esse negócio de ser companhia de seguros é vantajoso mesmo, hein...
