Função de Probabilidade e Função de Distribuição Acumulada
Produzido por Jorge Alberto NascimentoTeoria
Fala aí, seja bem vindo ao Responde Aí! Bora aprender o que é uma função de probabilidade e uma função de distribuição acumulada?!
📢 Clique para ver mais:
- Função de Probabilidade e Função de Distribuição Acumulada: Exercícios Resolvidos
- Introdução à Variável Aleatória Discreta
- Tabela Distribuição Normal
Função de Probabilidade
A função de probabilidade associa cada valor que a variável aleatória
Onde
-Oii?? Queee? 😖
Por exemplo, vamos considerar o evento do lançamento de duas moedas e a gente quer saber quantas caras foram obtidas. Nesse caso existem
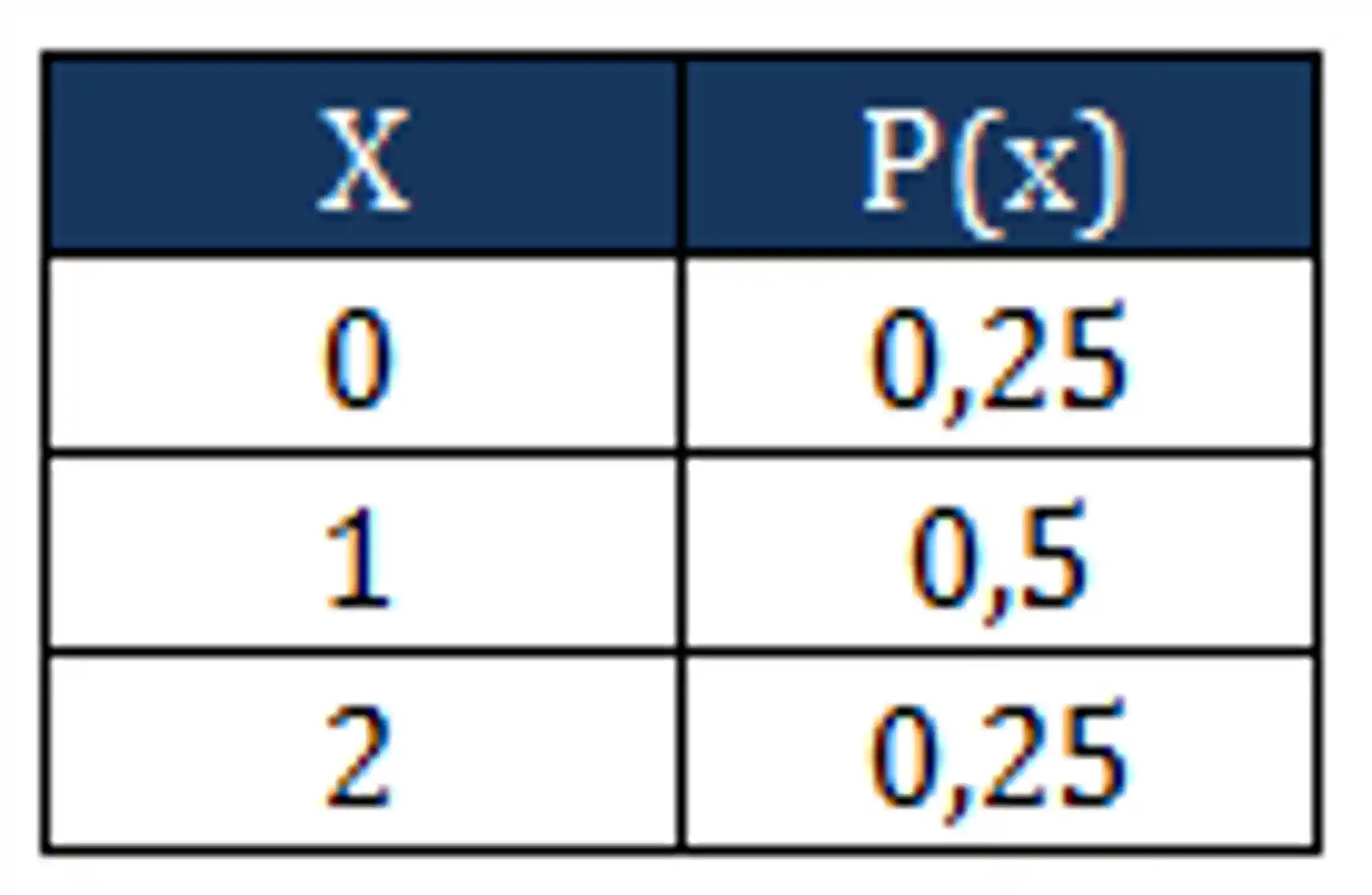
Nesse nosso exemplo a variável aleatória é a quantidade de caras que podem cair. Na tabela acima relacionamos a v.a.
Também podemos escrever a função de probabilidade da seguinte forma:
Sempre que quisemos a função de probabilidade de uma v.a. discreta podemos montar nossa tabelinha, identificando os possíveis valores que nossa v.a. pode assumir e as respectivas probabilidades.
Você também pode conferir esse conteúdo em vídeo:
Função de Distribuição Acumulada
A função de distribuição acumulada pode ser calculada pela seguinte fórmula:
Pra entender melhor como funciona a FDA, vamos voltar no exemplo do lançamento de duas moedas. Primeiro com vamos fazer
Como
Vamos fazer a mesma coisa para os valores
Por fim
O gráfico de
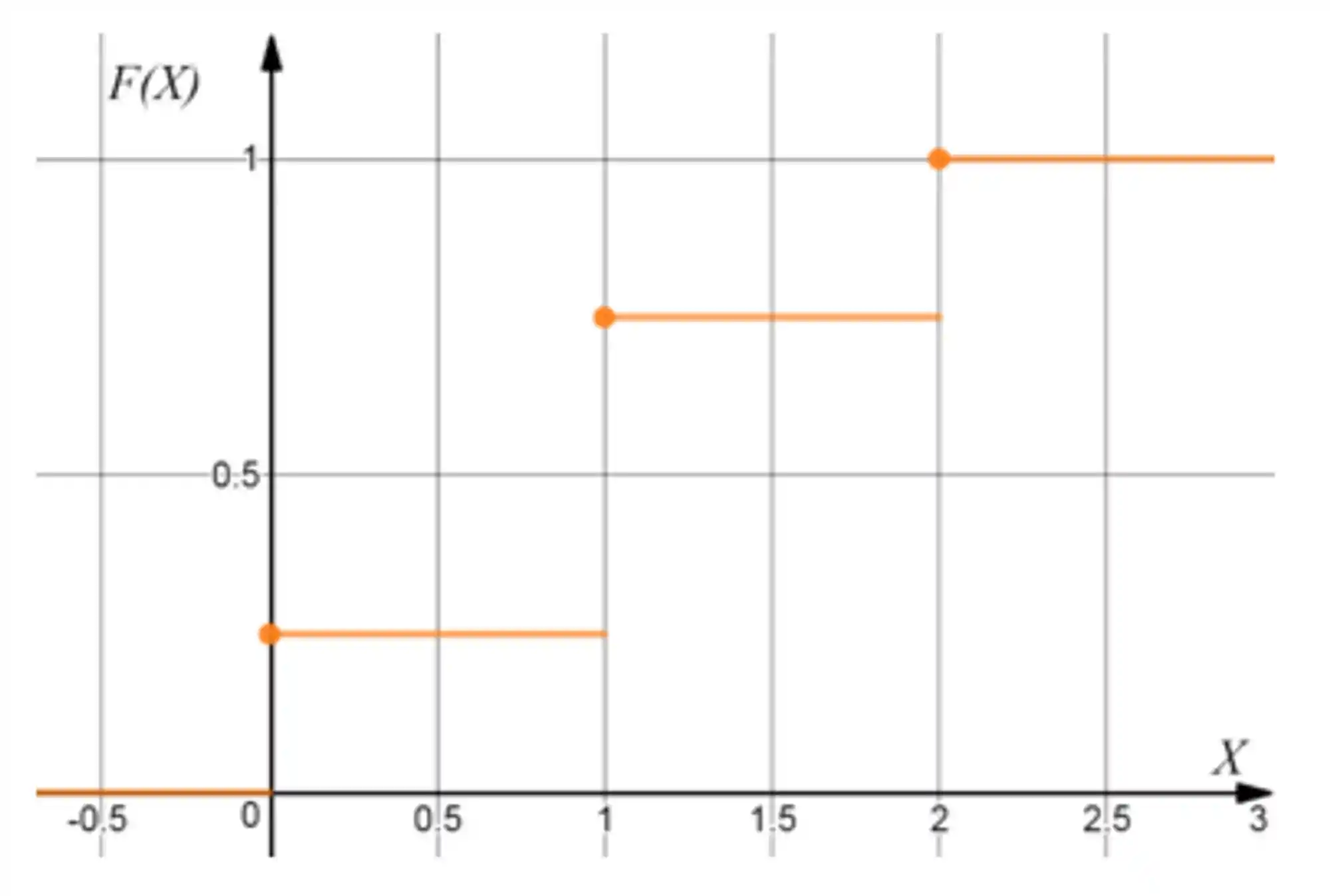
Bora fazer mais um exemplo? Então se liga no vídeo abaixo:
Agora vamos praticar com exercícios?