Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Distribuição Probabilidade Conjunta

Ver Todos os Exercícios

Teoria

Usamos a probabilidade conjunta quando queremos analisar mais de uma variável aleatória de um evento probabilístico. Por exemplo, imagina que o final de semana chegou e você tá doido por uma praia, mas pra dar praia você precisa dar seguintes condições:

  • Calor;
  • Tempo firme, sem chuva;

Nesse caso se você quiser calcular a probabilidade de dar praia você tem que considerar a probabilidade de fazer calor E não chover, então você tem que considerar uma variável aleatória bidimensional no seu cálculo de probabilidade! 😱

Mas sem desespero! vamos entender melhor como funciona essa Distribuição da Probabilidade Conjunta?!

📢 Clique pra ver mais:

Probabilidade Conjunta

Pra a gente aprender na prática como funciona a probabilidade conjunta a gente vai usar um exemplo! Imagina que você não aguenta mais essa vida de só estudar e quer encontrar um amor! 😍

Mas você é exigente e quer que essa pessoa tenha no máximo 2 defeitos e 3 qualidades! Nesse caso podemos escrever as variáveis da seguinte forma:

ú
ú

Podemos atribuir valores a essa variável:

Ou seja:

Onde e são os possíveis valores de e .

Você também pode conferir esse conteúdo em vídeo:

Como Calcular a Probabilidade Conjunta

A primeira coisa que precisamos pra calcular a probabilidade conjunta é de todas as combinações possíveis entre e . O melhor jeito de organizar dados de variáveis bidimensionais é usando uma tabela como a abaixo.

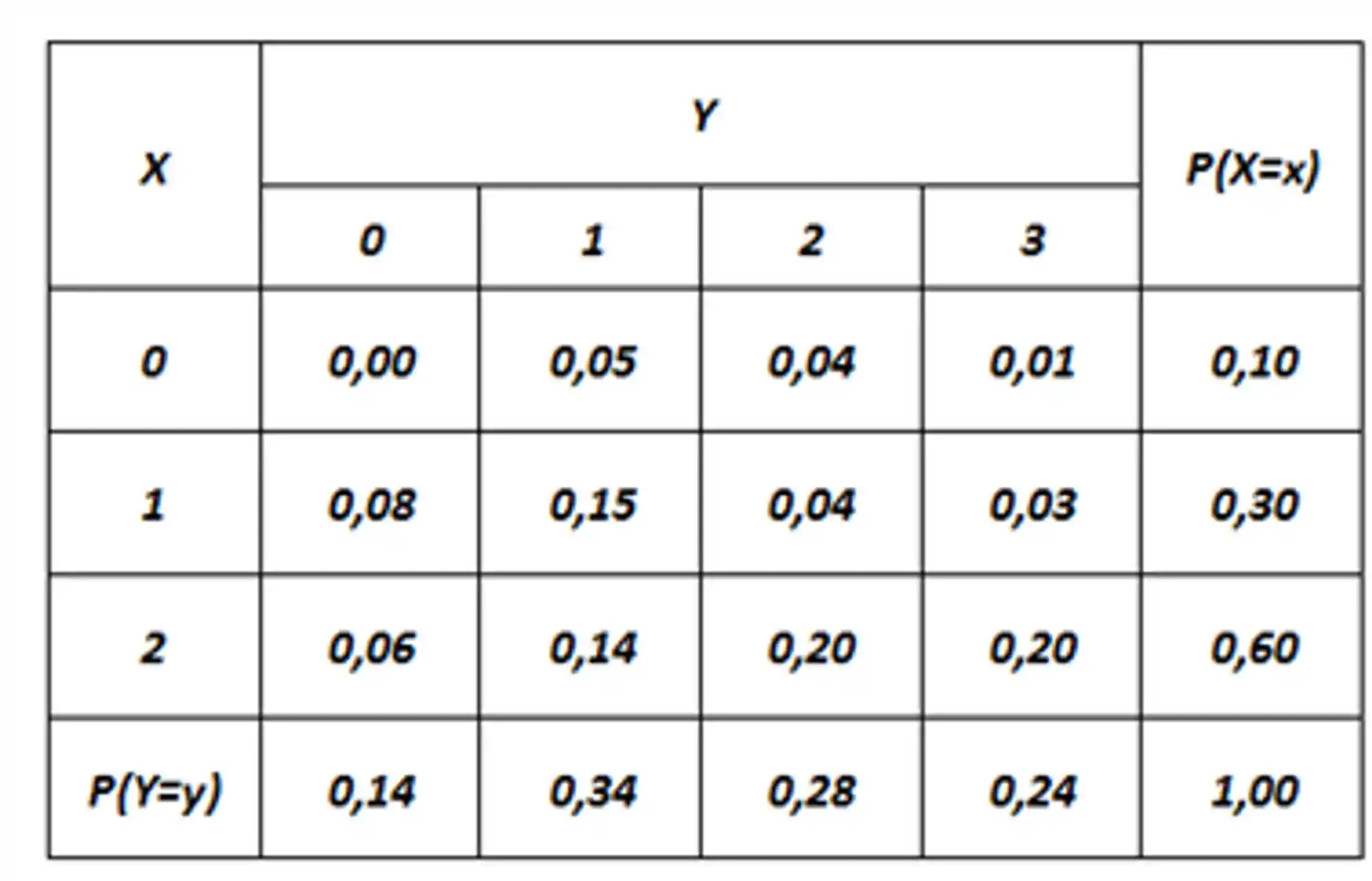
Combinações da variável bidimensional
Combinações da variável bidimensional

Agora é só cruzar os dados! Nesse caso a probabilidade de alguém ter qualidades e defeitos é de . E a probabilidade da pessoa ter zero defeitos e qualidades é de . Mas a análise não é tão simples assim, também temos que considerar a distribuição marginal!

Distribuição Marginal

A última linha e coluna da tabela acima representa a distribuição marginal, essa distribuição define a distribuição individual de cada característica. Isso é:

nos diz os valores totais da probabilidade de assumir cada um de seus valores possíveis. Então, por exemplo: é a probabilidade total de uma pessoa ter nenhum defeito, tendo ou qualidades. O mesmo raciocínio serve pra característica .

Beleza, e se agora eu quisesse saber a probabilidade de uma pessoa ter qualidades sabendo que ela tem defeitos? Nesse caso usamos a probabilidade condicional! Fazemos:

O raciocínio e a fórmula são as mesmas.

Essa interseção que a gente tem ali é a probabilidade da pessoa ter dois defeitos e três qualidades ao mesmo tempo. E essa probabilidade tá na nossa tabela! É o valor do cruzamento da linha com a coluna .


A probabilidade tá na nossa distribuição marginal, é o valor final da linha do . Dessa forma:

Independência das Variáveis Bidimensionais

Para verificarmos a independência das variáveis bidimensionais usamos a mesma lógica da independência dos eventos:

Nesse caso se e são independentes, então:

Então por exemplo, se então e são independentes? NÃO! Você tem que tentar todas as combinações possíveis, porque se isso não valer pra caso então já não são independentes.

Prontinho! Agora vamos praticar com exercícios?

Como Calcular a Probabilidade Conjunta

Independência das Variáveis Bidimensionais

Exercícios Resolvidos

Exercício Resolvido #1

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 206-01

Lançam-se, simultaneamente, uma moeda e um dado.

a) Determine o espaço amostral correspondente a esse experimento.

b) Obtenha a tabela da distribuição conjunta, considerando X o número de caras no lançamento da moeda e Y o número da face do dado.

d) Calcule:

  1. P X = 1
  2. P X ≤ 1
  3. P X < 1
  4. P(X=2,Y=3)
  5. P ( X ≥ 0 , Y ≤ 4 )
  6. P ( X = 0 , Y ≥ 1 )

Passo 1

Queremos o espaço amostral ( Ω ) . Vamos olhar separadamente:

  • Moeda: Ω M = K , C
  • Dado: Ω D = { 1,2 , 3,4 , 5,6 }

Portanto o espaço amostral são as possibilidades de combinação desses dois outros conjuntos correto?

Ω = { K 1 , K 2 , K 3 , K 4 , K 5 , K 6 , C 1 , C 2 , C 3 , C 4 , C 5 , C 6 }

Passo 2

Queremos montar a tabela agora considerando X o número de caras (K) no lançamento da moeda e Y o número da face do dado:

Analisando X:

Analisando Y:

Passo 3

Montando a tabela teremos:

Passo 4

d) Vamos calcular algumas probabilidades:

  1. P X = 1

    2. Como X é o número de caras no lançamento do dado, queremos a probabilidade de obter uma cara ou seja

    P X = 1 = 1 2

  2. P ( X ≤ 1 )

    3. Como X é o número de caras no lançamento do dado, queremos a probabilidade de dois casos: X = 0 → N ã o   s a i r   c a r a ,   s a i r   c o r o a ou X = 1 → S a i r   c a r a .Ou seja, estamos falando das duas possíveis ocorrências ao lançar uma moeda, portanto:

    P X ≤ 1 = 1

  3. P ( X < 1 )

    4. Como X é o número de caras no lançamento do dado, queremos a probabilidade de X < 1 ou seja de X = 0 → n ã o   s a i r   c a r a .

    P X < 1 = P X = 0 = 1 2

  4. P ( X = 2 , Y = 3 )

    5. Opa! Ele quer saber a probabilidade de X = 2 ! Mas isso não existe certo? Afinal lançamos a moeda apenas uma vez, não é possível obter duas caras!

    P X = 2 , Y = 3 = 0

  5. P ( X ≥ 0 , Y ≤ 4 )

    6. Primeira coisa que devemos olhar são quais eventos estão aí dentro:

    - P X ≥ 0 → P X = 0   e   P X = 1 → t o d a s   a s   p o s s i b i l i d a d e s

    - P Y ≤ 4 → P Y = 1 ,   P Y = 2 , P Y = 3   e   P ( Y = 4 )

    Então queremos

    P X = 0 , Y = 1 +   P X = 0 , Y = 2 + P X = 0 , Y = 3 +   P X = 0 , Y = 4 + P X = 1 , Y = 1 +   P X = 1 , Y = 2 + P X = 1 , Y = 3 +   P ( X = 1 , Y = 4 )

    Pela tabela é fácil localizar cada um desses termos, ex:

    P X = 0 , Y = 1 → 2 º   t e r m o   d a   2 ª   c o l u n a → 1 12

    Assim

    P X ≥ 0 , Y ≤ 4 = 8 × 1 12 = 2 3

  6. P ( X = 0 , Y ≥ 1 )

Agora vamos olhar apenas para os casos onde X = 0 e Y ≥ 1 .

Seguindo o mesmo raciocínio do item anterior teremos:

P X = 0 , Y ≥ 1 = P X = 0 , Y = 1 +   P X = 0 , Y = 2 + P X = 0 , Y = 3 +   P X = 0 , Y = 4 + P X = 0 , Y = 5 + P X = 0 , Y = 6 =

Pela tabela novamente localizamos esses termos, assim:

P X = 0 , Y ≥ 1 = 6 × 1 12 = 6 12 = 1 2

Resposta

a) Ω = { K 1 , K 2 , K 3 , K 4 , K 5 , K 6 , C 1 , C 2 , C 3 , C 4 , C 5 , C 6 }

b)

d)

  1. 1 2
  2. 1
  3. 1 2
  4. 0
  5. 2 3
  6. 1 2

Exercício Resolvido #2

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 210 - 08

Numa urna têm-se cinco bolas marcadas com os seguintes números: -1, 0, 0, 0, 1. Retiram-se três bolas, simultaneamente: X indica a soma dos números extraídos e Y o maior valor da trinca. Calcule:

a) A função de probabilidade de (X,Y).

Passo 1

A primeira coisa que iremos fazer é montar a tabela de distribuição tanto de X quanto de Y.

  • X: Indica a soma dos números extraídos:

    • Extraímos 3 bolas simultaneamente, portanto temos

    5 3 = 5 ! 3 ! 2 ! = 10   p o s s i b i l i d a d e s

    Nosso espaço amostral será:

    Passo 2

  • Y: O maior valor da trinca

Assim a tabela será:

Passo 2

Montando a tabela então teremos:

Para preencher o meio da tabela vamos olhar novamente para o espaço amostral:

Assim temos que:

P X = - 1 ,   Y = 0 = 3 10 = 0,3

P X = 0 ,   Y = 0 = 1 10 = 0,1

P X = 1 , Y = 0 = 0

P X = - 1 , Y = 1 = 0

P X = 0 , Y = 1 = 3 10 = 0,3

P X = 1 , Y = 1 = 3 10 = 0,3  

Completando a tabela teremos:

Resposta

Exercício Resolvido #3

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 210 - 07

Numa urna têm-se cinco tiras de papel, numeradas 1,3,5,5,7. Uma tira é sorteada e recolocada na urna, então uma segunda tira é sorteadas. Sejam X 1   e   X 2 o primeiro e o segundo números sorteados.

a) Determine a distribuição X 1   e   X 2

b) Obtenha as distribuições marginais de X 1   e   X 2

Passo 1

a) Determine a distribuição X 1   e   X 2

O primeiro passo é determinar o espaço amostral. Pelo enunciado temos um caso de retirada de urna, com reposição, portanto teremos:

Ω =

{ 1,1 ; 1,3 ; 1,5 ; 1,7 ; 3,1 ; 3,3 ; 3,5 ; 3,7 ; 5,1 ; 5,3 ; 5,5 ; 5,7 ; 7,1 ; 7,3 ; 7,5 ; 7,7 }

Passo 2

Analisando apenas a probabilidade da primeira retirada ( X 1 ) :

Como temos 5 possibilidades (1,3,5,5,7) podemos afirmar que

P X = 1 = P X = 3 = P X = 5 = P X = 7 = 1 5

Como temos duas tiras de papela do número cinco temos

P X = x = 2 5

Montando a tabela de distribuição marginal de X 1 .

Passo 3

Analisando apenas a probabilidade da segunda retirada ( X 2 ) :

Como temos 5 possibilidades (1,3,5,5,7), pois temos a reposição, podemos afirmar que

P X = 1 = P X = 3 = P X = 5 = P X = 7 = 1 5

Como temos duas tiras de papela do número cinco temos

P X = x = 2 5

Montando a tabela de distribuição marginal de X 2 .

Passo 4

Montando a tabela de distribuição de X 1   e   X 2 .

As distribuições marginais estão na última linha e na última coluna. Montamos a tabela de distribuição dos dois só para mostrar mesmo que elas SEMPRE vão aparecer e estar nas extremidades

Resposta

Exercício Resolvido #4

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 206-03

Considere a distribuição conjunta de X e Y, parcialmente conhecida, dada na tabela abaixo.

a) Complete a tabela, considerando X e Y independentes.

b) Obtenha as distribuições condicionais de X, dado que Y=0, e de Y, dado que X=1.

Passo 1

Primero passo é dar nome aos bois hehehe. Ou seja, vamos colocar em cada espaço vazio uma icognita.

A partir daí é só ir com calma e lembrar que a soma de uma linha/coluna tem que ser igual ao último valor da mesma

  • 2ª coluna:

    • 1 12 + d + 1 4 = i → i = 4 12 + d → i = 1 3 + d  

    Como eles são independentes, sabemos que

    i × 1 3 = d → i 3 = d → i = 3 d

    Substituindo na equação anterior teremos:

    3 d = 1 3 + d → 3 d - d = 1 3 → 2 d = 1 3 → d = 1 6

    Assim

    i = 3 d → i = 3 × 1 6 → i = 1 2

  • 2ª linha com 2ª coluna:

    • Podemos calcular c, pois por serem independentes sabemos que:

    i × c = 1 12 → 1 2 × c = 1 12 → c = 1 6

  • 5ª coluna:

    • Sabemos que a soma da 5ª coluna deve ser igual a 1, portanto

    c + 1 3 + h = 1 → 1 6 + 1 3 + h = 1 → h = 1 - 3 6 → h = 1 2

  • 4ª linha com 4ª coluna:

    • Podemos calcular k por serem independentes. Teremos:

    h × k = 1 4 → 1 2 × k = 1 4 → k = 1 2

  • 5ª linha

    • Sabemos que a soma da última linha deve ser igual a 1, portanto

    i + j + k = 1 → 1 2 + j + 1 2 = 1 → j = 0

  • 3ª coluna

    • Como descobrimos que j = 0 e sabemos que os eventos são independentes, teremos que:

    a = e = g = 0

  • 3ª linha com 4ª coluna

    • Por eles serem independentes podemos afirmar que:

    k × 1 3 = f → 1 2 × 1 3 = f → f = 1 6

  • 2ª linha com 4ª coluna

Por eles serem independentes podemos afirmar que:

k × c = b → 1 2 × 1 6 = b → b = 1 12

Substituindo na tabela teremos:

Passo 2

Para calcularmos a condicional precisamos lembrar da formulinha da probabilidade condicional. Vocês lembram?

P A B = P A ∩ B P B

Bom, sabemos na tabela que as probabilidades marginais representam a probabilidade de cada variável aleatória em um certo ponto, enquando os outros componentes das tabelas são das probabilidade conjuntas, da interseção.

Quando pedimos a distribuição condicional de X dado que Y=0 queremos:

P X = - 1 Y = 0

P X = 0 Y = 0

P X = 1 Y = 0

Simbora pras contas então?

  1. P X = - 1 Y = 0

    2. P X = - 1 Y = 0 = P X = - 1 , Y = 0 P Y = 0

    Olhando a tabela sabemos que P X = - 1 , Y = 0 = 1 6 , portanto

    P X = - 1 Y = 0 = P X = - 1 , Y = 0 P Y = 0 = 1 6 1 3 = 1 2

  2. P X = 0 Y = 0

    3. P X = 0 Y = 0 = P X = 0 , Y = 0 P Y = 0

    Olhando a tabela sabemos que P ( X = 0 , Y = 0 ) = 0 , portanto

    P X = 0 Y = 0 = P X = 0 , Y = 0 P Y = 0 = 0

  3. P X = 1 Y = 0

P X = 1 Y = 0 = P X = 1 , Y = 0 P Y = 0

Olhando a tabela sabemos que P X = 1 , Y = 0 = 1 6 , portanto

P X = 1 Y = 0 = P X = 1 , Y = 0 P Y = 0 = 1 6 1 3 = 1 2

Montando uma tabela teríamos:

Passo 3

Faremos o mesmo passo a passo para saber outra probabilidade condicional.

Dessa vez queremos saber a probabilidade condicional de Y dado X = 1 . Queremos:

P Y = - 1 X = 1

P Y = 0 X = 1

P Y = 1 X = 1

Vamos?

  1. P Y = - 1 X = 1

    2. Y = - 1 X = 1 = P X = 1 , Y = - 1 P X = 1

    Olhando na tabela vemos que P X = 1 , Y = - 1 = 1 12 , portanto

    Y = - 1 X = 1 = P X = 1 , Y = - 1 P X = 1 = 1 12 1 2 = 1 6

  2. P Y = 0 X = 1

    3. Olhando na tabela vemos que P X = 1 , Y = 0 = 1 12 , portanto

    Y = - 1 X = 1 = P X = 1 , Y = 0 P X = 1 = 1 6 1 2 = 1 3

  3. P Y = 1 X = 1

Olhando na tabela vemos que P X = 1 , Y = 1 = 1 4 , portanto

Y = - 1 X = 1 = P X = 1 , Y = 1 P X = 1 = 1 4 1 2 = 2

Montando uma tabela:

Resposta

a)

b)

Exercício Resolvido #5

UFRJ-P1-2012.1-5(a)

Uma urna contém 3 bolas brancas e 2 bolas vermelhas. Um experimento consiste em se extrair sequencialmente e sem reposição duas bolas e registrar suas cores. Seja X a v.a. que representa o número de bolas brancas retiradas nas duas extrações e seja Y a v.a. que assume 1 se a primeira bola extraída é branca e 0 se a primeira bola extraída é vermelha.

  1. Obtenha a distribuição conjunta de X   e Y através de uma tabela e diga se X   e Y são independentes, justificando. Sugestão: Na montagem da tabela, comece determinando as distribuições marginais de X   e de Y . Em seguida, obtenha P X = 0 ; Y = 1 e P ( X = 2 ; Y = 0 ) . Finalmente complete a tabela, respeitando as propriedades de uma distribuição conjunta.

Passo 1

(a)

A gente tem que montar nossa tabela marota.

Primeiro vamos entender melhor o problema.

X : n ú m e r o   d e   b o l a s   b r a n c a s   r e t i r a d a s   n a s   d u a s   e x t r a ç õ e s

X pode assumir os valores: 0(se não sair nenhuma branca nas duas), 1 ou 2.

Y : 1   ,                         s e   a   p r i m e i r a   b o l a   é   b r a n c a 0   ,               s e   a   p r i m e i r a   b o l a   é   v e r m e l h a

Bom, vamos seguir os conselhos do exercício.

Passo 2

Vamos começar com as distribuições marginais.

Começando por Y .

P Y = 0 = 2 5

Já que são 2 bolas vermelhas, num total de 5 bolas.

P Y = 1 = 3 5

Já que são 3 bolas brancas, num total de 5 bolas.

Passo 3

Agora vamos fazer a distribuição marginal de X .

P X = 0 = 2 5 × 1 4 = 1 10

Já que pra não sair nenhuma bola branca, na primeira retirada tem que sair uma vermelha, 2 / 5 , e na segunda também tem que sair uma vermelha, 1 / 4 (lembrando que é sem reposição).

P X = 1 = 3 5 × 2 4 + 2 5 × 3 4 = 6 10 = 3 5

Pra sair no total 1 branca, temos duas opções: sair branca na primeira (3/5) e vermelha na segunda (2/4) ooou sair vermelha na primeira (2/5) e branca na segunda (3/4).

Pra finalizar.

P X = 2 = 3 5 × 2 4 = 3 10

Pra sair 2 brancas, tem que sair uma branca na primeira (3/5) e uma branca na segunda (2/4).

Passo 4

Seguindo os conselhos do exercício, vamos calcular agora:

P X = 0 ; Y = 1 =   ?

Probabilidade de sair bola branca na primeira retirada e no total não sair nenhuma branca. HAM? Impossível, concorda?

Então:

P X = 0 ; Y = 1 = 0

Agora calcular, P X = 2 ; Y = 0 =   ?

Também é impossível, certo? Não dá pra sair duas bolas brancas se na primeira retirada sair uma vermelha. Então:

P X = 2 ; Y = 0 = 0

Passo 5

Vamos montar a tabela com os valores que a gente já tem.

Completando a tabela, lembrando que o somatório das linhas e das colunas tem que ser igual aos valores da distribuição marginal, a gente ficará com:

Pronto, era isso que a gente queria.

Passo 6

Agora pra ver se são independentes é ver se existe algum caso que não verifique a seguinte afirmação.

P X = x i , Y = y i = P ( X = x i ) × P ( Y = y i )

Nesses casos é bom olhar pra exemplos que tenham 0 na tabela, fica mais tranquilo verificar. Por exemplo:

P X = 2 , Y = 0 = 0

P X = 2 × P Y = 0 = 3 10 × 2 5

Então,

P ( X = 2 , Y = 0 ) ≠ P ( X = 2 ) × P ( Y = 0 )

E com isso dizemos que X e Y não são independentes.

Resposta

a   n ã o   s ã o   i n d e p e n d e n t e s

Exercícios de Livros Relacionados

Uma urna contém inicialmente 1 bola vermelha e 1 bola azul. Em cada rodada, uma bola é retirada aleatoriamente e substituída por duas outra bolas de mesma cor (por exemplo, se a bola vermelha ê a prim
Uma pilha do tipo C está em condição de trabalho com probabilidade 0,7 , enquanto uma pilha do tipo D está em condição de trabalho com probabilidade 0,4. Uma piIha é selecionada aleatoriamente de um c
Sorteiam-se bolas de uma urna que contém inicialmente 20 bolas vermelhas e 10 bolas azuis.(a) Qual é a probabilidade de que todas as bolas vermelhas sejam retiradas antes de todas as azuis?Agora supon
No Exemplo 3 f , suponha que a nova evidência esteja sujeita a possíveis interpretaçōes e de fato mostre que é apenas 90 % provável que o criminoso possua a característica em questão. Neste caso, qual
Suponha que 5 % dos homens e 0,25 % das mulheres sejam daltônicos. Uma pessoa daltônica é escolhida aleatoriamente. Qual é a probabilidade dessa pessoa ser um homem? Suponha que exista um mesmo número