Uma barra de metal cujo coeficiente de condutibilidade térmica é de , tem de comprimento e seção transversal de área . A barra está termicamente isolada nas laterais, tendo uma extremidade imersa em gelo fundente (0°C) e outra em vapor de água fervente (100°C).
Determine o fluxo de calor conduzido ao longo da barra
Passo 1
Opa faaala ai, vamos continuar com nossos exercícios de propagação de calor!
Bora começar separando essas informações ai!Temos:Condutibilidade térmica
Comprimento
Seção transversal (que é a área olhando de frente da barra)
Temperaturas
Passo 2
Shooow, agora que demos nome aos bois, vamos lembrar da nossa fórmula do fluxo
Que podemos escrever assim
Beleza, temos tudo que precisamos pra achar esse fluxo, só precisamos substituir e fazer umas continhas, então vamo lá!
Multiplicando o com o
podemos simplificar um dos zeros do com o do
Multiplicando o com o
Fazendo essa divisão, chegamos em
Passo 3
Mas vamos achar a unidade aqui! Nossa equação é
Analisando só as unidades temos
Vamos ver o que podemos cortar!!
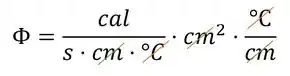
O que sobrar no final é a nossa unidade do fluxo de calor 😊
Então nossa resposta final é