Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Velocidade Média

Ver Todos os Exercícios

Teoria

Fala aí, tudo bem?

Vamos bater um papo sobre cinética química?

Cinética tem tudo a ver com velocidade, ela se preocupa em responder “quanto tempo essa reação leva pra acontecer”.

Algumas reações são espontâneas, mas levam anos pra acontecer. Outras, ocorrem assim que os reagentes entram em contato: são espontâneas e imediatas.

Mas como que a gente pode definir a velocidade de uma reação? Como afirmar se ela é rápida ou não?

Vem comigo pra gente ver isso aí!

Velocidade Média

Se um carro anda 30 km em 1 hora, a gente pode dizer que sua velocidade é 30   k m / h ! Mas e pra reações, como a gente define a velocidade dela?

Quando a gente faz uma reação normalmente nosso objetivo é produzir produtos!

Imagina isso:

O 2 ( g ) + 2 M g ( s ) → 2 M g O ( s )

Eu to reagindo magnésio com oxigênio pra produzir óxido de magnésio.

A gente pode definir a velocidade ( v ) da uma reação como a variação na concentração de M g O no meio ( ∆ [ M g O ] ) em determinado intervalo de tempo ( ∆ t ).

v = ∆ [ M g O ] ∆ t

Então, de uma maneira mais genérica, a velocidade de uma reação é definida como a variação na concentração de produto em um intervalo de tempo!

v = ∆ [ P ] ∆ t

Por outro lado, os reagentes também são consumidos nesse mesmo intervalo de tempo, certo? Posso definir a velocidade através deles? Pode sim, senhor!

Como a concentração de reagente diminui com o tempo, a fórmula da velocidade em relação aos reagentes ganha um sinal de menos, uma vez que a velocidade é positiva.

v = - ∆ [ R ] ∆ t

Considerando as unidades mais comuns de concentração são m o l L ou g L , e as unidades de tempo mais usadas são segundo ou hora, a velocidade de reação pode ser dada em:

m o l L . s ou g L . h ou m o l L . h

E também outras variações, de acordo com as unidades que você tiver ou forem pedidas!

Ao invés de concentração, a gente também pode usar quantidade. Tipo assim.. número de mols por minuto ao invés de mols por litro são produzidos por minuto.

v = ∆ n P ∆ t = - ∆ n R ∆ t

Onde n é o número de moles de produto ou reagente, show de bolinha?

Essa é a velocidade média de consumo de determinado reagente ou de produção de determinado produto em dado intervalo de tempo.

Velocidade da Reação

Agora vamos pensar como isso funciona na prática, vamos olhar de novo praquela reação do começo!

O 2 ( g ) + 2 M g ( s ) → 2 M g O ( s ) Assim que a gente mistura os reagentes, no instante t = 0   s , ainda não tem produto na nossa mistura, então M g O = 0 . Mas não precisa passar muito tempo pra gente já ter alguma coisa formada!

Olha essa tabelinha com as concentrações dos reagentes e do produto no tempo 0 e no tempo 2 segundos:

Calculando a velocidade de formação do M g O :

v = ∆ [ P ] ∆ t = 1,0 - 0 2 = 0 , 50   m o l L . s

A velocidade de consumo de oxigênio:

v = - ∆ R ∆ t = - 0,5 - 1,0 2 = 0,25   m o l L . s

Já a velocidade de consumo de magnésio:

v = - ∆ R ∆ t = - 1,0 - 2,0 2 = 0,50   m o l L . s

Ai você deve estar se perguntando: as velocidades são diferentes, e agora? Qual velocidade eu uso? Não tinha que ser tudo igual?

Aguenta ai que eu vou te responder!

As velocidades são diferentes porque os coeficientes estequimétricos são diferentes! Então, faz todo sentido que a velocidade de consumo do magnésio seja o dobro da velocidade de consumo do oxigênio, já que pra cada mol de O 2 e gente precis de 2 moles de M g . Beleza?

E aí, que velocidade a gente deve usar pra representar a reação?

Pra resolver essa questão, a gente vai juntar tudo que a gente viu ali em cima e fazer a velocidade média da reação.

E como que funciona essa história de velocidade média da reação? Ela leva em conta os coeficientes estequiométricos!

Vamos pensar comigo o seguinte: você tá na fila do bandejão e tem 3 moças servindo a comida. Não importa se duas delas forem super rápidas, se pelo menos 1 dela for devagar, a fila vai andar devagar, certo? Então a velocidade da fila fica limitada pela menor velocidade das moças que estão servindo.

Pras reações vai acontecer a mesma coisa, a menor velocidade limita a velocidade de reação!

Então se a velocidade de consumo de O 2 é 0,25   m o l L . s e a velocidade de consumo do M g é 0,50   m o l L . s , a velocidade da reação vai ser 0,25   m o l L . s .

Então pra generalizar o que a gente acabou de ver, se liga nisso aqui!

Dada uma reação qualquer do tipo:

a A + b B → c C + d D

A velocidade média da reação é definida como:

v r e a ç ã o = - 1 a . ∆ A ∆ t = - 1 b . ∆ B ∆ t = 1 c . ∆ C ∆ t = 1 d . ∆ [ D ] ∆ t

Viu? Aquela história de sinal de menos para os reagentes e sem menos para os produtos segue valendo!

Mas agora a gente divide a velocidade individual da substância pelo coeficiente dela na reação balanceada. E calcula uma velocidade única para a reação como um todo.

Obs: às vezes, as pessoas falam só velocidade da reação ao invés de velocidade média da reação, se referindo à mesma coisa.

Agora, velocidade de produção de tal produto ou de consumo de tal reagente pode ser diferente da velocidade média da reação, beleza?

Vamos praticar?

Velocidade da Reação

E aí, que velocidade a gente deve usar pra representar a reação?

Exercícios Resolvidos

Exercício Resolvido #1

Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 562-Exemplo 14.1.

Suponha que estamos estudando a reação 2 H I ( g ) → H 2 ( g ) + I 2 ( g ) e que descobrimos que no intervalo de 100 s a concentração de H I decresceu de 4,00   m m o l . L - 1 para 3,50   m m o l . L - 1 . Qual é a velocidade média da reação?

Passo 1

Dada a reação balanceada:

2 H I ( g ) → H 2 ( g ) + I 2 ( g )

A gente viu que a velocidade média da reação é:

v m é d i a =   - 1 2 . ∆ H I ∆ t = 1 1 . ∆ H 2 ∆ t = 1 1 . ∆ [ I 2 ] ∆ t

E como só temos os dados em relação ao H I , é essa partezinha da fórmula que vamos usar.

v m é d i a =   - 1 2 . ∆ H I ∆ t

Passo 2

Substituindo as informações fornecidas no enunciado:

v m é d i a =   - 1 2 . ∆ H I ∆ t = - 1 2 . 3,50 - 4,00 100 = 0 , 5 2 00 = 0,005 2 = 0,0025 m m o l L . s

v m é d i a = 2,5 . 10 - 3 m m o l L . s

Aquele m m o l equivale a 10 - 3 m o l . Então a gente “embelezar” nossa resposta assim:

v m é d i a = 2,5   μ m o l L . s

Resposta

v m é d i a = 2,5   μ m o l L . s

Exercício Resolvido #2

Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 563-Teste 14.2A. Modificado.

A velocidade média da reação N 2 ( g ) + 3 H 2 ( g ) → 2 N H 3 ( g ) , durante um certo tempo, é registrada como 1,15   m m o l   N H 3 . L - 1 . h - 1 .

a) Qual é a velocidade, no mesmo período de tempo, em termos do desaparecimento de H 2 ?

b) Qual é a velocidade média única?

Passo 1

Fala aí! Belezinha? Bom, esse enunciado quer duas coisas da gente: a primeira é a velocidade do desaparecimento de H 2 , no período de tempo dado, e a segunda é a velocidade média única, tranquilo?

Então vamos começar relembrando como achar a velocidade média de uma reação, ok?

v m é d i a = ∆ P r o d u t o s ∆ t

Mas existe um outro jeito, a velocidade média também pode ser:

v m é d i a = - ∆ R e a g e n t e s ∆ t

Esse negativo aí na frente é porque quando trabalhamos com o reagente, temos que ter em mente que a concentração dele vai diminuir no decorrer da reação, beleza?

Passo 2

O enunciado deu pra gente, que a velocidade média da reação, em um certo tempo, é de:

v m é d i a = 1,15   m m o l   N H 3 / L . h

A nossa reação produz o N H 3 , certo? Então a velocidade média é exatamente a velocidade de geração desse cara, pela reação, beleza? Isso também fica claro quando vemos esse   m m o l   N H 3 na unidade!

Ele está nos indicando que estamos falando da velocidade de produção do produto N H 3 , nessa reação, ok?

Isso quer dizer que:

∆ [ N H 3 ] ∆ t

E o que ele quer é a velocidade do desaparecimento do H 2 , que é um dos produtos... Pela fórmula da velocidade da reação, nós podemos dizer que:

v m é d i a = - ∆ N 2 ∆ t = - 1 3 . ∆ H 2 ∆ t = 1 2 .   ∆ [ N H 3 ] ∆ t

Detalhando cada termo, temos:

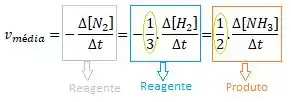
Essas frações marcadas em verde, nos indicam o coeficiente estequiométrico do H 2 e do N H 3 , respectivamente.

Agora tudo ficou mais claro, né? Então, bora calcular!

Passo 3

a) Sabendo que:

∆ N H 3 ∆ t = 1,15   m m o l L . h

A gente pode substituir em:

- 1 3 . ∆ H 2 ∆ t = 1 2 .   ∆ [ N H 3 ] ∆ t

E ai fica assim:

- 1 3 . ∆ H 2 ∆ t = 1 2 .   1,15

- ∆ H 2 ∆ t = 1 2 . 3 1   1,15

v H 2 = - ∆ H 2 ∆ t = 1,72   m m o l   H 2 . L - 1 . h - 1

Passo 4

b) Pra velocidade média única (aquela da reação):

v m é d i a = - ∆ N 2 ∆ t = - 1 3 . ∆ H 2 ∆ t = 1 2 .   ∆ [ N H 3 ] ∆ t

Usando o que já calculamos:

v m é d i a = - 1 3 . 1,72 = 1 2 .   1,15 = 0,57   m m o l L . h

Resposta

a) v H 2 = 1,72   m m o l   H 2 . L - 1 . h - 1

b) v m é d i a = 0,57   m m o l . L - 1 . h - 1

Exercício Resolvido #3

Elaboração própria.

Para a reação:

N 2 O 5 ( g ) → N O 2 ( g ) + O 2 ( g )

a) Balanceia a reação pelo método das tentativas.

b) Com os dados da tabela abaixo, calcule as velocidades médias da reação para os intervalos de 0 a 2 segundos, 2 a 4 segundos, 0 a 4 segundos.

Passo 1

a) Pelo método das tentativas, procuramos um elemento que se encontre apenas em um substância em ambos os lados, e fixamos seu coeficiente.

Vamos, portanto, escolher o nitrogênio e fixar seu coeficiente igual a 1, onde seu índice é maior. No caso, o índice do nitrogênio é maior no N 2 O 5 do que no N O 2 .

1 N 2 O 5 ( g ) → N O 2 ( g ) + O 2 ( g )

Com dois nitrogênios nos reagentes, precisamos de dois nitrogênios nos produtos.

1 N 2 O 5 ( g ) → 2 N O 2 ( g ) + O 2 ( g )

E pelo número de oxigênios, vemos que o gás oxigênio tem que tem coeficiente ½.

1 N 2 O 5 ( g ) → 2 N O 2 ( g ) + 1 2 O 2 ( g )

Mas uma reação devidamente balanceada deve estar com coeficientes inteiros. Portanto, vamos multiplicar essa equação aí de cima por dois, obtendo:

2 N 2 O 5 g → 4 N O 2 g + 1 O 2 g

Show!!

Passo 2

b) A velocidade média da reação, de acordo com nossa reação balanceada, será:

2 N 2 O 5 g → 4 N O 2 g + O 2 g

v = - 1 2 . ∆ N 2 O 5 ∆ t = 1 4 .   ∆ N O 2 ∆ t = ∆ [ O 2 ] ∆ t

Como temos os dados das concentrações de todas as substâncias, você pode escolher qualquer uma delas pra fazer as contas!

O bom de fazer com mais de uma é poder conferir o resultado, uma vez que a resposta deve ser sempre a mesma, claro.

Passo 3

Para o intervalo de 0 a 2 segundos:

v = - 1 2 . ∆ N 2 O 5 ∆ t = 1 4 .   ∆ N O 2 ∆ t = ∆ [ O 2 ] ∆ t

v = - 1 2 . 0,60 - 0,80 2 = 1 4 .   0,40 - 0,00 2 = 0,10 - 0,00 2 = 0,05   m o l L . s

Para o intervalo de 2 a 4 segundos:

v = - 1 2 . ∆ N 2 O 5 ∆ t = 1 4 .   ∆ N O 2 ∆ t = ∆ [ O 2 ] ∆ t

v = - 1 2 . 0,50 - 0,60 2 = 1 4 .   0,60 - 0,40 2 = 0,15 - 0,10 2 = 0,025   m o l L . s

E para o intervalo de 0 a 4 segundos:

v = - 1 2 . ∆ N 2 O 5 ∆ t = 1 4 .   ∆ N O 2 ∆ t = ∆ [ O 2 ] ∆ t

v = - 1 2 . 0,50 - 0,80 4 = 1 4 .   0,60 - 0,00 4 = 0,15 - 0,00 4 = 0,037   m o l L . s

Resposta

a) 2 N 2 O 5 g → 4 N O 2 g + O 2 g

b) v 0 → 2 = 0,05   m o l . L - 1 . s - 1

        v 2 → 4 = 0,025   m o l . L - 1 . s - 1

        v 0 → 4 = 0,037   m o l . L - 1 . s - 1

Exercício Resolvido #4

Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 602-14.1.

Complete as afirmações seguintes, relativas à produção de amônia pelo processo de Haber, cuja reação total é:

N 2 ( g ) + 3 H 2 ( g ) → 2 N H 3 ( g )

a) A velocidade de desaparecimento de N 2 é _______ vezes a velocidade de desaparecimento de H 2 .

b) A velocidade de formação de N H 3 é _______ vezes a velocidade de desaparecimento de H 2 .

c) A velocidade de formação de N H 3 é _______ vezes a velocidade de desaparecimento de N 2 .

Passo 1

a) Olhando pra reação, a gente vê que, pela estequiometria estabelecida entre N 2 e H 2 , ao consumir um mol de N 2 , 3 mols de H 2 são consumidos.

Ou seja, a velocidade de consumo do H 2 é três vezes a velocidade de de consumo do N 2 . O que nos leva a:

“A velocidade de desaparecimento de N 2 é 1 3 vezes a velocidade de desaparecimento de H 2 .”

Também poderíamos fazer pela fórmula da velocidade da reação:

v r e a ç ã o = - ∆ N 2 ∆ t = - 1 3 . ∆ H 2 ∆ t = 1 2 .   ∆ [ N H 3 ] ∆ t

v r e a ç ã o = v ( N 2 ) = 1 3 . v ( H 2 ) = 1 2 .   v ( N H 3 )

De onde a gente vê que:

v ( N 2 ) = 1 3 . v ( H 2 )

Passo 2

b) Agora entre H 2 e N H 3 a relação é um pouco menos nítida só pela equação química.

Mas usando a fórmula da velocidade da reação, a gente vê que:

v r e a ç ã o = v ( N 2 ) = 1 3 . v ( H 2 ) = 1 2 .   v ( N H 3 )

1 3 . v ( H 2 ) = 1 2 .   v ( N H 3 )

2 3 . v ( H 2 ) = v ( N H 3 )

Ou seja:

“A velocidade de formação de N H 3 é 2 3 vezes a velocidade de desaparecimento de H 2 .”

Passo 3

c) Pela reação química a gente vê que a cada mol de N 2 consumido, dois de N H 3 são produzidos. Portanto:

“A velocidade de formação de N H 3 é 2 vezes a velocidade de desaparecimento de N 2 .”

O que também pode ser averiguado por:

v r e a ç ã o = v ( N 2 ) = 1 3 . v ( H 2 ) = 1 2 .   v ( N H 3 )

v ( N 2 ) = 1 2 .   v ( N H 3 )

2 v ( N 2 ) = v ( N H 3 )

Resposta

a) 1/3

b) 2/3

c) 2

Exercício Resolvido #5

Elaboração própria.

Observe o gráfico abaixo, que traça a concentração de determinada substância em função do tempo em um reator.

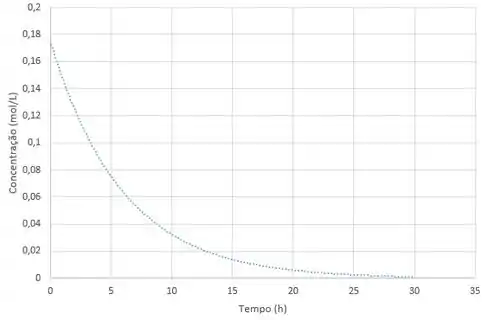
Com base no gráfico, responda:

a) A substância em questão é um reagente ou produto da reação que se procede no reator?

b) Qual a velocidade média, em relação a essa substância, nas 30 primeiras horas?

c) Determine a velocidade instantânea no tempo t = 5   h .

d) Determine a velocidade instantânea no tempo t = 10   h .

e) Considerando que o a curva de concentração x tempo obedeça a função 0,1749 e - 0,169 x , calcule a velocidade instantânea no tempo igual a 10 h.

Passo 1

a) Pelo gráfico a gente pode ver que a concentração da substância diminui com o passar do tempo. Portanto, a substância está sendo consumida (e não produzida) no meio.

A substância é um reagente.

Passo 2

b) Para a substância em questão, temos:

            t = 0   h                   s u b s t â n c i a ≈ 0,175   m o l / L

t = 30   h               s u b s t â n c i a ≈ 0,0   m o l / L

Portanto, a velocidade média em relação a essa substância pode ser calculada por:

v = - ∆ [ s u b s t â n c i a ] ∆ t

Não esquece do menos, porque estamos falando de um reagente!

v = - ∆ s u b s t â n c i a ∆ t = - 0,0 - 0,175 30 = 5,83 . 10 - 3 m o l L . h

Passo 3

c) A velocidade instantânea é dada pela tangente da curva, no instante determinado.

Por exemplo, no instante t = 5   h , podemos traçar a tangente à curva, assim:

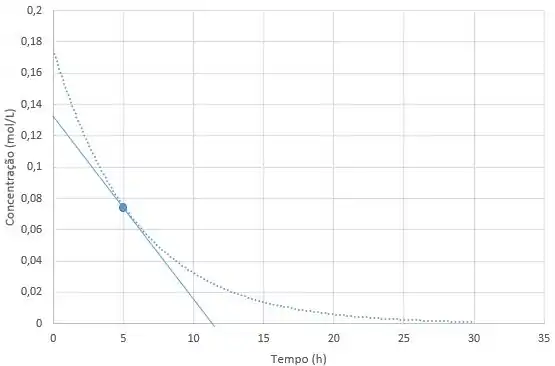
Claro que esse é um método aproximado. Mas dessa forma, podemos calcular a velocidade instantânea, que será dada pelo coeficiente angular da reta que a gente acabou de traçar.

c o e f i c i e n t e   a n g u l a r = ∆ y ∆ x ≈ - 0,135 11 = - 0,012

Tal que a velocidade de consumo desse reagente no instante t = 5 h é 1,2 . 10 - 2   m o l / L . h .

Observe que uma velocidade de consumo negativa seria o mesmo que estar produzindo o cara, por isso usamos a velocidade positiva!

Passo 4

d) Para o tempo t = 10   h , mesmo procedimento!

Começamos traçando a curva tangente no ponto.

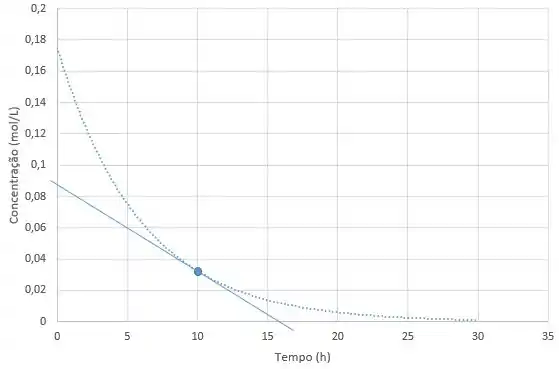
c o e f i c i e n t e   a n g u l a r = ∆ y ∆ x ≈ - 0,087 15,7 = - 0,0055 = - 5,5 . 10 - 3

Tal que a velocidade de consumo desse reagente no instante t = 10 h é 5,5 . 10 - 3   m o l / L . h .

Passo 5

e) Se a gente conhece exatamente a função que representa a relação entre a concentração e o tempo, podemos calcular a velocidade instantânea pela derivada dessa função!!

Então, bora derivar:

y = 0,1749 e - 0,169 x

y ' = - 0,169   .   0,1749 . e - 0,169 x

E o valor da derivada para x = t = 10   h :

y ' = - 0,169   .   0,1749 . e - 0,169 . 10 = - 0,0054

Tal que a velocidade de consumo desse reagente no instante t = 10 h é 5,4 . 10 - 3   m o l / L . h .

A diferença do valor calculado nos itens d e e deve-se às aproximações feitas no item d.

Resposta

a) Reagente

b) v = 5,83 . 10 - 3   m o l . L - 1 . h - 1

c) v = 1,2 . 10 - 2   m o l . L - 1 . h - 1

d) v = 5,5 . 10 - 3   m o l . L - 1 . h - 1

e) v = 5,4 . 10 - 3   m o l . L - 1 . h - 1

Exercício Resolvido #6

James E. Brady e Gerard E. Humiston Volume 2, 2ª edição: Livros Técnico Científicos Editora. página 485 exercício 12.43

Para a reação,

4 N H 3 ( g ) + 3   O 2 ( g )   → 2   N 2 ( g ) + 6   H 2 O ( g )

Foi encontrado que, num determinado instante, o N 2 era formado a uma velocidade de 0,68   m o l . d m - 3 . s - 1

  1. A que velocidade a água era formada?
  2. A que velocidade o   N H 3 reagia?
  3. A que velocidade era o O 2 consumido?

Passo 1

Velocidade de formação da água

Para mandar bem nesse tipo de questão é muito importante estar a tento que há uma proporção entre a cada espécie química seja ela consumida ou seja ela formada e essa proporção está presente na própria reação química já balanceada.

Pela reação temos que:

2   N 2 - - - - - - - - - 6   H 2 O ( g )

0,68   m o l . d m - 3 . s - 1 - - - - - - - - - X

Logo:

X = 2,04 m o l . d m - 3 . s - 1

Passo 2

Velocidade de consumo da N H 3

Mantendo a relação estequiométrica temos que:

4 N H 3 ( g ) - - - - - - - - 2   N 2 ( g )

X - - - - - - - - 0 , 68   m o l . d m - 3 . s - 1

Logo:

X = 1,36 m o l . d m - 3 . s - 1

Passo 3

Velocidade de consumo do O 2

Mais uma vez vamos lançar uma regra de três, sempre tendo atenção aos coeficientes da reação.

3   O 2 g - - - - - - - 2   N 2 ( g )

X - - - - - - - - 0,68   m o l . d m - 3 . s - 1

Logo:

X = 1 , 02 m o l . d m - 3 . s - 1

Resposta

Velocidade de formação da água

X = 2,04 m o l . d m - 3 . s - 1

Velocidade de consumo da amônia

X = 1,36 m o l . d m - 3 . s - 1

Velocidade de consumo do oxigênio

X = 1,02 m o l . d m - 3 . s - 1

Exercício Resolvido #7

James E. Brady e Gerard E. Humiston Volume 2, 2ª edição: Livros Técnico Científicos Editora. página 485 exercício 12.42

Considere a reação para a combustão do metano ( C H 4 ):

C H 4 ( g ) + 2   O 2 ( g )   → C O 2 ( g ) + 2   H 2 O ( g )

Se o metano é queimado a uma velocidade de 0,16   m o l . d m - 3 . s - 1 , a que velocidades são formados o C O 2 e H 2 O ?

Passo 1

Velocidade de formação do C O 2

A resolução desse tipo de questão está muito presa a estequiometria da equação dada. Nesse caso a reação química já veio balanceada, mas caso não tivesse seria o primeiro passo, e o mais importante também.

Agora vamos usar a proporção da reação para prever a as quantidades formadas de C O 2   e H 2 O

Pela reação temos que:

C H 4 ( g ) - - - - - - - - - - C O 2 ( g )

0,16   m o l . d m - 3 . s - 1 - - - - - - - - - X

Logo:

X = 0,16 m o l . d m - 3 . s - 1

Como a proporção é de 1:1 então as velocidade de consumo de metano e formação do C O 2 são as mesmas

Passo 2

Velocidade de formação da água

Pela reação temos que:

C H 4 ( g ) - - - - - - - - - - 2   H 2 O ( g )

0,16   m o l . d m - 3 . s - 1 - - - - - - - - - X

Logo:

X = 0,32 m o l . d m - 3 . s - 1

Resposta

Velocidade de formação da   C O 2

X = 0,16 m o l . d m - 3 . s - 1

Velocidade de formação da água

X = 0,32 m o l . d m - 3 . s - 1

Exercícios de Livros Relacionados

14.5- (a) O dióxido de nitrogênio, N O 2 , decompõe-se com 6,5m m o l / L.s na reação 2N O 2( g )→2N O( g )+O 2( g ) . Determine a velocidade de formação de O 2 . (b) Qual é a velocidade única da reaç
14.6- Os íons manganato, MnO42-, reagem em solução ácida com 2 mol/L . min-1 para formar íons permanganato e óxido de manganês (IV) 3 MnO42- (aq) + 4 H+ (aq) → 2 MnO 4-(aq) + MnO2 (s) + 2 H2O (l). (a)
(a) Na reação 3 ClO- (aq) → 2 Cl- (aq) + ClO3- (aq) , a velocidade de formação de Cl- é 3,6 mol/ L . min-1. Qual é a velocidade de reação de ClO- ? (b) Qual é a velocidade única da reação ?
A decomposição do gás peróxido de oxigênio, 2N 2 O 5 ( g ) →4 N O 2 ( g ) +O 2 ( g ) , dá, em 298 K, os seguintes resultados:Use programas de computação gráfica padronizados para lançar em gráfico a c
A decomposição do gás iodeto de hidrogênio, 2H I ( g ) →H 2 ( g ) +I 2 ( g ) , dá, em 700 K, os seguintes resultados:Use programas de computação gráfica padronizados para lançar em gráfico a concentra