Regressão Linear
Produzido por Juliana EcheniqueTeoria
Introdução
Em química analítica, muitas vezes vamos estar lá no laboratório fazendo um experimento, e vamos precisar fazer uma análise em cima dos resultados que obtivemos. Uma das análises mais comuns nessa área é a regressão linear. Com ela, nós conseguiremos fazer com que os nossos dados seja aproximado por uma reta.
Imagine que você tenha que titular uma série de soluções padrões e anotar o volume de titulante usado. Os resultados você anotou na tabelinha abaixo:

Com esses valores, nós conseguimos colocar eles em um gráfico da seguinte forma:
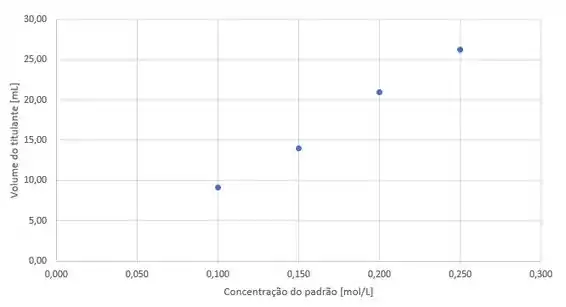
O nosso objetivo, com a regressão linear, vai ser encontrar a reta que mais se aproxima de todos os pontos que encontramos. O gráfico abaixo mostra a melhor reta que representa os dados encontrados em nosso experimento:

Método dos mínimos quadrados
Para conseguir encontrar a equação dessa reta, podemos usar o método dos minímos quadrados. Esse método tem como principal objetivo encontrar a reta que minimiza o quadrado dos erros, isto é, a o quadrado da diferença entre os pontos experimentais e a reta aproximada. Sendo assim, precisaremos encontrar uma reta do tipo:
Onde é o coeficiente angular (inclinação da reta) e 1= o coeficiente linear (interseção no eixo ). Como eu disse, essa reta tem que ser aquela que minimiza os erros, ou resíduos. A soma dos quadrados dos resídiuos pode ser encontrada pela equação abaixo:
Precisamos então fazer com que seja o menor possível, porque aí estaremos diminuindo os erros. Não vamos entrar no desenvolvimento matemático disso muito profundamente, mas vamos direto ao ponto.
A partir da equação acima, é possível chegar em três outras que vêm dela e que usaremos para calcular os coeficientes da nossa reta:
Sendo que e são os valores médios de e .
Com esses três valores, podemos calcular e da seguinte forma:
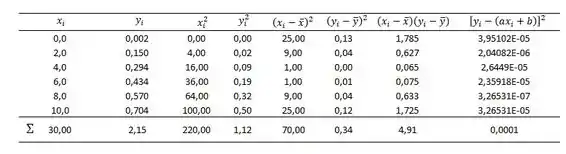
Vamos ver como ficaria para o nosso exemplo. Vamos fazer uma tabelinha para não nos perder:
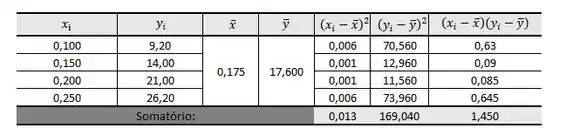
Portanto:
Vamos calcular os coeficientes da reta agora:
Portanto, a reta que mais se aproxima dos dados obtidos no nosso experimento é:
Desvios padrões e intervalos de confiança
Com os valores de , e também podemos calcular quatro tipos de desvio padrão da nossa reta:
- Desvio padrão da regressão :
- Desvio padrão da inclinação () e intervalo de confiança ():
- Desvio padrão da interseção () e intervalo de confiança ():
- Desvio padrão dos resultados obtidos a partir da curva de calibração () e intervalo de confiança ():
Para encontrar o intervalo de confiança da inclinação basta aplicar a fórmula:
Com intervalo de confiança:
Essa última é a expressão que indica o erro que obteremos caso utilizemos a equação de reta encontrada para encontrar um novo valor. Nessa equação é o valor obtido na reta, é o número de replicatas e é o número de pontos na reta.
E um intervalo de confiança de um valor obtido através da equação da reta:
Coeficiente de correlação
Uma das principais formar de determinar se uma reta é uma boa representação do conjunto de pontos obtidos é através do coeficiente de correlação (). Quanto mais perto o valor de for de melhor terá sido a regressão linear. O valor de pode ser encontrado da seguinte forma:
Onde é a soma dos quadrados dos resíduos que definimos no início:
E é a soma dos quadrados dos erros em :
Vamos adicionar uma linha na nossa tabela para calcular :

Sendo assim, temos:
Portanto, podemos calcular :
O valor encontrado é muito próximo de e bastante satisfatório também. Geralmente, valores de maiores que já são ótimos.
Desvios padrões e intervalos de confiança
Coeficiente de correlação
Exercícios Resolvidos
Exercício Resolvido #1
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 8, Questões e Problemas 8-16. Adaptado.
Os dados na tabela que segue foram obtidos durante uma determinação colorimétrica de glicose em soro sangüíneo.
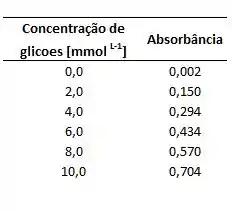
Faça a regressão linear, encontre a equação da reta pelo método dos mínimos quadrado e determine o coeficiente de correlação.
Passo 1
Para começar, vamos primeiro definir que a concentração de glicose será nosso e os valores de absorbância serão o nosso :

Para fazer a análise dos mínimos quadrados, também precisamos das médias de e , então vamos calculá-las:
Passo 2
Além das médias, também é importante calcular os quadrados e os quadrados das diferenças dos valores, assim como suas somas. Sendo assim, vamos expandir nossa tabela de apoio:
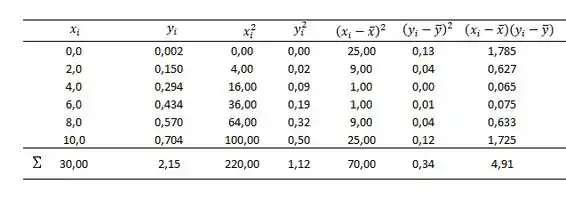
Com o auxílio dessa tabela podemos determinar:
E com isso, já conseguiresmo determinar os coeficientes da reta:
Como nossa reta é do tipo:
Ela será então:
Passo 3
Para calcular precisaremos de mais uma coluna na nossa tabela, a coluna de .
Como:
Logo:
O coeficiente de correlação pode ser calculado através da seguinte fórmula:
Onde:
Portanto:
Resposta
Exercício Resolvido #2
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 8, Questões e Problemas 8-17. Adaptado.
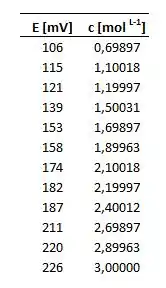
Os dados na tabela a seguir representam o potencial de eletro verus a concentração .

- Transforme os dados em valores de versus
- Acha a equação da reta da regressãp linear de versus
- Encontre o coeficiente de correlação.
Passo 1
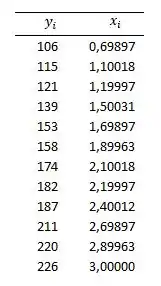
Primeiramente, devemos transformar nossos dados na coluna da concentração. Para obter uma relação linear entre os dois dados, precisaremos aplicar em todos os valores de concentração. Sendo assim, nossa nova tabela, será:
Passo 2
Agora, já poderemos começar a aplicar o método dos mínimos quadrados. Vamos chamar o potencial do eletro de e de .
Podemos também calcular os valores de e :
Passo 3
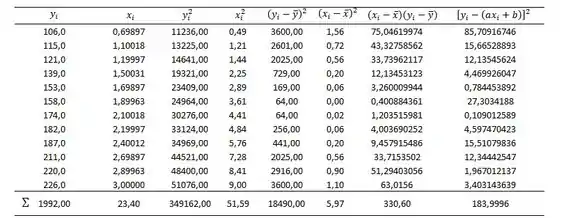
Além das médias, também é importante calcular os quadrados e os quadrados das diferenças dos valores, assim como suas somas. Sendo assim, vamos expandir nossa tabela de apoio:

Com o auxílio dessa tabela podemos determinar:
E com isso, já conseguiresmo determinar os coeficientes da reta:
Como nossa reta é do tipo:
Ela será então:
Passo 4
Para calcular precisaremos de mais uma coluna na nossa tabela, a coluna de :
Como:
Logo:
O coeficiente de correlação pode ser calculado através da seguinte fórmula:
Onde:
Portanto:
Resposta
Exercício Resolvido #3
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 8, Questões e Problemas 8-13. Adaptado.
A concentração do íon sulfato em águas naturais pode ser determinada pela medida da turbidez que resulta quando um excesso de BaCl2 é adicionado a uma quantidade medida da amostra. Um turbidímetro, instrumento usado para essa análise, foi calibrado com uma série de padrões de soluções padrão de Na2SO4. Os seguintes dados foram obtidos na calibração:

- Encontre a equação da reta através do método dos mínimos quadrados.
- Encontre o coeficiente de correlação,
- Para uma leitura no turbidímetro de , qual seria a concentração de sulfato?
Passo 1
Precisamos então aplicar o método dos mínimos quadros nos dados que o enunciado nos deu para conseguir calcular nossa regressão linear. Antes de começar a fazer qualquer coisa, vamos definir a concentração de sulfato como nossa variável independente () e a leitura do turbidímetro como a variável dependente ():
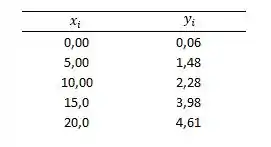
Com isso, vamos calcular nossos valores médios, e :
Passo 2
Além das médias, também é importante calcular os quadrados e os quadrados das diferenças dos valores, assim como suas somas. Sendo assim, vamos expandir nossa tabela de apoio:
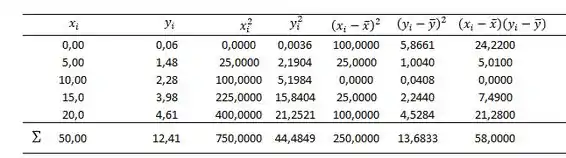
Com o auxílio dessa tabela podemos determinar:
E com isso, já conseguiresmo determinar os coeficientes da reta:
Como nossa reta é do tipo:
Ela será então:
Passo 3
Para calcular precisaremos de mais uma coluna na nossa tabela, a coluna de .
Como:
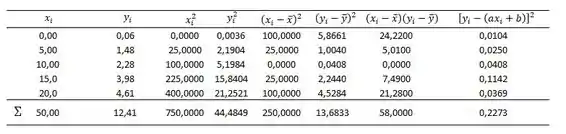
Logo:
O coeficiente de correlação pode ser calculado através da seguinte fórmula:
Onde:
Portanto:
Passo 4
Por fim, precisamos estimar qual seria a concentração da amostra se a leitura no turbidímetro fosse de . Para isso, vamos usar a equação da reta que encontramos:
Como a leitura é , temos que:
Jpgando na equação da reta:
Resposta
Exercício Resolvido #4
UFJF – Instituto de Ciências Exatas – Departamento de Química – QUI 154/150 – Aula 1 – Introdução à Química Analítica Instrumental Parte 2. Exemplo 2. Adaptado
Na determinação de um fármaco por fluorescência em meio ácido, foram obtidos os seguintes resultados:
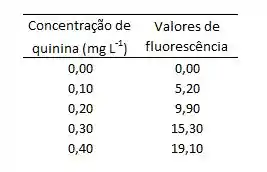
- Calcule o valor de e a equação da reta
- Considerando que a intensidade de uma amostra foi de , calcule o valor de quinina na amostra
- Calcule os desvio padrões e os intervalos de confiança a da inclinação e da interseção da reta.
Passo 1
Para começar, vamos primeiro definir que a concentração de quinina será nosso e os valores de fluorescência serão o nosso :
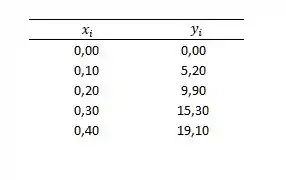
Para fazer a análise dos Mínimos quadrados, também precisamos das médias de e , então vamos calculá-las:
Passo 2
Além das médias, também é importante calcular os quadrados e os quadrados das diferenças dos valores, assim como suas somas. Sendo assim, vamos expandir nossa tabela de apoio:
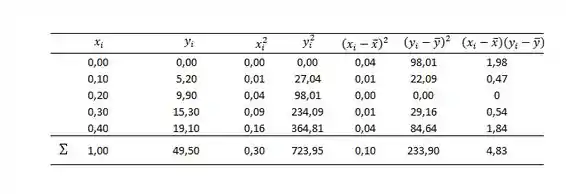
Com o auxílio dessa tabela podemos determinar:
E com isso, já conseguiresmo determinar os coeficientes da reta:
Como nossa reta é do tipo:
Ela será então:
Passo 3
Para calcular precisaremos de mais uma coluna na nossa tabela, a coluna de :

Como:
Logo:
O coeficiente de correlação pode ser calculado através da seguinte fórmula:
Onde:
Portanto:
Passo 4
Caso a intensidade de fluorescência em uma amostra fosse de , ou seja, nosso valor de , para achar a concentração da amostra, precisamos apenas aplicar esse valor na equação da reta encontrada, que foi:
Passo 5
Agora devemos calcular o desvio padrão e intervalo de confiança para a inclinação e a interseção. Para calular isso, primeiro precisamos calcular o desvio padrão da regressão () conforme a fórmula abaixo:
Com , pois é o número de pontos. Sendo assim, o desvio padrão da regressão será:
Para a inclinação, o desvio padrão será:
E o intervalo de confiança:
Onde é o coeficiente com grau de liberdade 2 graus menor que o número de pontos e nível de confiança de . Consultando uma tabela, teremos:
Portanto:
Para a interseção, a fórmula do desvio padrão é:
Usando os valores da tabela:
E o intervalo de confiança é calculado de maneira análoga:
Resposta
Exercício Resolvido #5
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 8, Exemplo 8-4. Adaptado.
Desenvolva uma análise de mínimos quadrados dos dados fornecidos pelas duas primeiras colunas da tabela abaixo que representa os dados obtidos na calibração para a determinação cromotográfica do isoctano em uma mistura de hidrocarbonetos
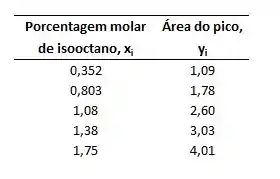
Passo 1
Bom pessoal, quando a questão pede para a gente fazer a análise do método dos mínimos quadrado, isso significa que a gente precisa fazer TUDO. Ou seja, calular a reta, o coeficiente de correlação, as variâncias e os intervalos de confiança.
Vamos começar então pelos médias:
Passo 2
Com os valores das médias, conseguiremos calcular tudo que precisamos na nossa tabela para então começar a fazer os nosso cálculos:
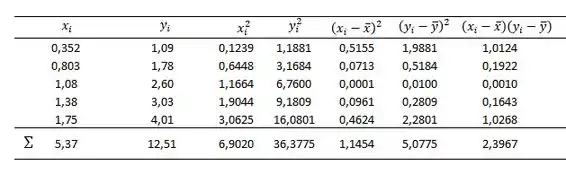
Com o auxílio dessa tabela podemos determinar:
E com isso, já conseguiresmo determinar os coeficientes da reta:
Como nossa reta é do tipo:
Ela será então:
Passo 3
Vamos partir agora para o cálculo nosso coeficiente de correlação, . Para isso, precisaremos de mais uma coluna na nossa tabela, a coluna de .
Como:
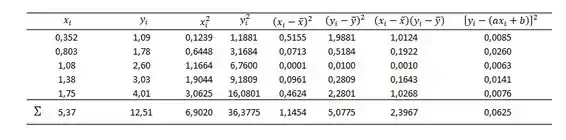
Logo:
O coeficiente de correlação pode ser calculado através da seguinte fórmula:
Onde:
Portanto:
Passo 4
Agora precisaremos calcular as variâncias e os intervalos de confiança do coeficiente angular e do coeficiente linear.
Porém, antes disso, precisaremos da variância da regressão, ela é dada por:
Substituindo os valores, teremos:
Passo 5
Vamos calular agora a variância do coeficiente angular (:
Substituindo tudo:
Com a variância de , podemos calcular seu intervalo de confiança, pela fórmula abaixo:
Onde é tem grau de liberdade duas unidades menor que oo número de pontos, ou seja, três. Como o enunciado não determinou o nível de confiança, vamos fazer para que é o nível de confiança mais usual. O valor de para grau de liberdade e nível de confiança é de . Portanto, nosso intervalo de confiança será:
Passo 6
Vamos fazer o mesmo agora para o coeficiente angular :
Substituindo na fórmula:
O intervalo de confiança será portanto: