Teste de Hipóteses
Produzido por Juliana EcheniqueTeoria
Imagina que você fez seus experimentos e fez uma média dos resultados, mas você conhece pela literarura um resultado teórico e seu objetivo é se aproximar ao máximo desse valor!
Existem algumas possibilidades, a primeira é que o seu resultado seja exatamente igual ao resultado experimental:
Chamamos esta de hipótese nula e representamos com o . Mas caso essa hipótese não seja verdadeira, exisem outras formas de enxergar o resultado, podemos ter:
Onde é chamada de hipótese alternativa!
A gente já sabe que em um experimento podem vir erros de todos os lugares! E que eles são divididos em erros sistemáticos e erros aleatórios e que os erros aleatórios podem ser previstos pela curva de distribuição normal.
Teste z
Você ta em um laboratório e quer determinar a energia de ativação de uma reação química, então realiza o mesmo experimento vezes e tira uma média dos resultados, e calcula um desvio padrão de .
Porém na literatura o valor da energia de ativação é , ai você se pergunta, “o valor que eu achei é razoável?”
É ai que entra o teste !!
Podemos usar o teste sempre que tivermos um grande número de resultados, dessa forma o desvio padrão da amostra é uma boa estimativa para o desvio padrão da população , o pode ser calculado por:
Mas vamos passo a passo!
A nossa hipótese nula é:
Mas já sabemos que ela não é real, então vamos escrever a hipótese alternativa, :
Afinal não estamos interessados em particular se ou , só queremos saber o quanto ele é diferente!
Vamos calcular o então:
“Ok, mas o que esse valor me diz? O resultado do meu experimento é ou não razoável?!”
Isso, meu caro, vai depender do nível de confiança que você determinar! Vamos rever uma tabelinha que apareceu pra a gente lá em Limites de Confiança:
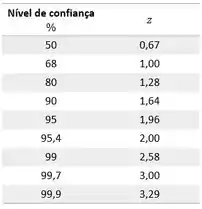
Vamos supor que o nosso limite de confiança seja de , o , pra sabermos se vamos rejeitar ou não os valores vamos ver se:
Nesse caso temos , então vamos rejeitar os valores!
Resuminho
- Escrever a hipótese nula
- Calcular
- Determinar a hipótese alternativa e a região de rejeição:
Para , rejeitar se ou
Para , rejeitar se
Para , rejeitar se
Teste
Sou só eu ou você também achou loucura repetir o mesmo experimento vezes?! Haahah
Pois é, muitas vezes é complicado ter acesso a uma amostra tão grande, então para uma amostra pequena a gente vai usar o teste !
Agora que já entendemos o espirito da coisa, vamos direto para o passo a passo:
- Escrever a hipótese nula
- Calcular
- Determinar a hipótese alternativa e a região de rejeição:
Para , rejeitar se ou
Para , rejeitar se
Para , rejeitar se t
Vamos pegar o mesmo exemplo, mas dessa vez vamos considerar que o teste tenha sido feito em triplicata, ou seja, vezes!
A hipótese nula continua sendo a mesma:
Dessa vez achamos a média e o desvio padrão . Calculando :
Agora a gente consulta outra tabelinha que também vimos lá atrás:

Se o número de amostras é , então temos graus de liberdade, portanto para um nível de confiança de
Então temos:
Então a hipótese nula é válida!!
Teste F
O teste é um pouquinho diferente, usamos ele para comparar a variância de dois conjuntos de dados!
A gente escreve assim:
Onde e são os desvio padrão de dois conjuntos de dados, sendo que o desvio padrão no numerador deve ser sempre o maior, de forma que .A hipótese nula é:
A hipótese nula deve ser descartada se se afastar muito de .
Não existe a opção , já que o maior desvio padrão deve ficar no numerador.
Onde e são o desvio padrão das duas séries de dados, e a expressão é arranjada de forma que seja sempre maior que , ou seja, a maior variância fica no numerador e a menor no denominador.
Após calcularmos , devemos consultar a seguinte tabela:
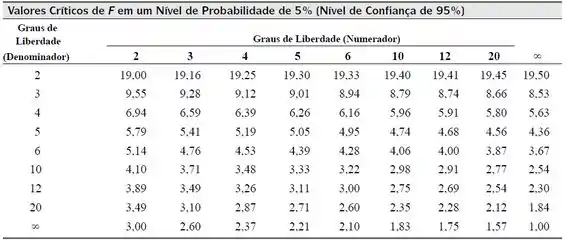
Essa tabela é para um nível de confiança de , com ela a gente acha . Se então consideramos a hipótese nula verdadeira.