Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 11.Exercícios - Ex. 13a

13a – Escreva os determinantes seculares para (a) o antreceno, (b) o fenantreno, admitindo as aproximações de Hückel e usando os orbitais C2p como base.

Passo 1

Vamos começar revendo como se escreve um determinante secular seguindo a aproximação de Hückel.

O determinante secular pela aproximação de Hückel tem a seguinte forma:

x 1 1 x 0 … 1 … 0 1 0 0 0 1 … … x 1 … … … 0 … … … … 1 0 … … 0 … … 1 1 x

Onde,

x = α - E β

O determinante tem a forma de uma matriz N x N, onde N é o nº de átomos de carbono na molécula do composto, para este caso.

Passo 2

Vamos agora contabilizar os átomos de carbono nas moléculas do antraceno e fenantreno.

A molécula de antraceno é:

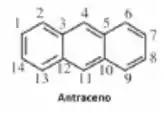
Você pode ver pela imagem acima que na molécula do antraceno tem-se 14 átomos de carbono, logo o determinante secular com base nas aproximações de Hückel é:

x 1 1 x 0 0 1 0 0 0 0 0 0 0 0 1 0 0 x 1 1 x 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 x 1 0 1 0 x 1 1 x 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 x 1 1 x 0 0 1 0 0 0 0 0 0 0 0 1 0 0 x 1 1 x 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 x 1 0 1 0 x 1 1 x

Lembrando que

x = α - E β

Passo 3

Vamos agora para o antraceno.

A molécula de fenantreno é dada por:

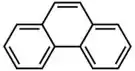
Esta molécula também tem 14 átomos de carbono, assim:

x 1 1 x 0 0 1 0 0 0 0 0 0 0 0 1 0 0 x 1 1 x 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 x 1 0 1 0 x 1 1 x 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 x 1 1 x 0 0 1 0 0 0 0 0 0 0 0 1 0 0 x 1 1 x 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 x 1 0 1 0 x 1 1 x

x = α - E β

Resposta

Antraceno e Fenantreno:

x 1 1 x 0 0 1 0 0 0 0 0 0 0 0 1 0 0 x 1 1 x 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 x 1 0 1 0 x 1 1 x 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 x 1 1 x 0 0 1 0 0 0 0 0 0 0 0 1 0 0 x 1 1 x 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 x 1 0 1 0 x 1 1 x

x = α - E β

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As matrizes unidimensionais D(C3) = 1 e D(C2) = 1, e as matrizes D(C3) = 1 e D(C2) = -1 representam ambas a multiplicação C3C2 = C6 no grupo C6V com D(C6) = + 1 e -1, respectivamente. Confirme essa ob
O produto xyz é necessariamente evanescente quando integrado sobre (a) um cubo, (b) um tetraedro, (c) um prisma hexagonal, cada qual centrado na origem?
Um estudo computacional sobre os compostos AMX, em que A é um elemento do grupo 14 da tabela periódica e M um metal alcalino, mostra muitos desvios em relação às estruturas mais simétricas de cada fór
B.A. Bovenzi e G.A. Pearse, Jr. Sintetizaram compostos de coordenação do ligante tridentado piridina-2,6-diamidoxima (C7H9N5O2, figura abaixo). A reação com NiSO4 leva a um complexo que tem os dois li
Numa investigação espectroscópica do C60, cientistas localizaram picos no espectro de fluorescência. A molécula tem simetria icosaédrica (Ih). O estado eletrônico fundamental é A1g, e os estados excit