Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 12.Exercícios - Ex. 1a

1a – A molécula CH3Cl pertence ao grupo C3v. Dê os elementos de simetria do grupo e localize-os na molécula.

Passo 1

Vamos relembrar quais são os eixos de simetria que classificam e identificam cada grupo pontual molecular.

Cada elemento de simetria está relacionado com uma certa operação de simetria. Temos o elemento eixo de simetria n-ário, Cn, relacionado com a operação rotação n-ária, o elemento plano especular, σ, relacionado com a reflexão, o elemento centro de simetria, i, associado com a operação de inversão, e por último, temos o elemento de simetria eixo de rotação impróprio n-ário, Sn, associado com a operação de rotação imprópria n-ária.

Passo 2

Para sabermos quais são os elementos de simetria, precisamos conhecer a geometria da molécula, e usando o fluxograma da figura 12.7 do Atkins, sabendo qual grupo tal molécula pertence, conseguimos identificar quais elementos ela possui.

A molécula de CH3Cl possui uma geometria tetraédrica, conforma a imagem abaixo:

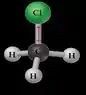
Uma molécula que pertence ao grupo, Cnv, possui como elementos de simetria, o elemento de identidade E, 1 eixo de simetria, Cn, e nσv, plano de simetria vertical.

Passo 3

Seguindo, então, o fluxograma da figura 12.7, e com base nas informações contidas no Atkins, será apresentado a seguir os elementos de simetria e onde estes estão localizados.

A molécula CH3Cl tem:

-O elemento de identidade E;

-1 eixo de simetria C3 para a ligação C-Cl;

-3 planos de espelho (especulares) verticais, σv, definidos pelos três planos das ligações ClCH.

Resposta

-O elemento de identidade E;

-1 eixo de simetria C3 para a ligação C-Cl;

-3 planos de espelho (especulares) verticais, σv, definidos pelos três planos das ligações ClCH.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8a – Identifique os grupos a que pertencem os seguintes corpos: a) esfera; b) triangulo isósceles; c) triangulo equilátero; d) lápis cilíndrico sem ponta.

7a – O grupo D2 é constituído pelos elementos E, C2, C2’ e C2”, onde os três eixos de rotação binaria são mutuamente perpendiculares. Monte a tabela de multiplicação desse grupo.

5a – Mostre que a função xy é do tipo de simetria B2 no grupo C4v.

12a – Imagine a molécula de NO2 do C2v. A combinação px(A) – px(B) dos dois átomos de O (com x perpendicular ao plano) cobre A2. Há algum orbital do átomo de N central que possa ter superposição não-n

15a – Seja f1 = sen(θ) e f2 = cos(θ). Mostre, por simetria, usando o grupo C5, que a integral do produto das duas, sobre um intervalo simétrico em torno do θ = 0, é nula.