Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 12.Exercícios - Ex. 5a
5a – Mostre que a função xy é do tipo de simetria B2 no grupo C4v.
Passo 1
Vamos precisar dos caracteres para o grupo C4v especificamente para a espécie de simetria B2 para verificarmos os seus respectivos caracteres.
Pela seção de dados do Atkins:
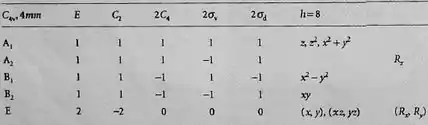
Passo 2
Como você pode ver na imagem anterior, os elementos de simetria do grupo C4v são C2, C4, σv, σd, além do elemento identidade E. a função xy possui um comportamento intrínseco para cada uma das operações de simetria representadas por cada elemento de simetria. Para todos os elementos de simetria, em relação ao eixo x, temos que o valor de x é igual a 1. Para o eixo y, para os elementos, E, C2 e σd, o valor de y é igual a 1, enquanto para os demais seus valores são 1 negativo, assim para cada elemento de simetria teremos:
-Para o elemento E:
-Para o elemento C2:
-Para o elemento C4:
-Para o elemento σv:
-Para o elemento σd:
Em comparação, os valores de xy são os mesmos para o tipo de simetria B2.
Resposta
-Para o elemento E:
-Para o elemento C2:
-Para o elemento C4:
-Para o elemento σv:
-Para o elemento σd: